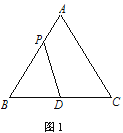
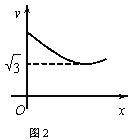
【题目】如图1,在等边△ABC中,D是BC的中点,P为AB 边上的一个动点,设AP=x,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则△ABC的面积为( )
A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()
参考答案:
【答案】D
【解析】
由图1、图2结合题意可知,当DP⊥AB时,DP最短,由此可得DP最短=y最小=![]() ,这样如图3,过点P作PD⊥AB于点P,连接AD,结合△ABC是等边三角形和点D是BC边的中点进行分析解答即可.
,这样如图3,过点P作PD⊥AB于点P,连接AD,结合△ABC是等边三角形和点D是BC边的中点进行分析解答即可.
由题意可知:当DP⊥AB时,DP最短,由此可得DP最短=y最小=![]() ,如图3,过点P作PD⊥AB于点P,连接AD,
,如图3,过点P作PD⊥AB于点P,连接AD,
∵△ABC是等边三角形,点D是BC边上的中点,
∴∠ABC=60°,AD⊥BC,
∵DP⊥AB于点P,此时DP=![]() ,
,
∴BD=![]() ,
,
∴BC=2BD=4,
∴AB=4,
∴AD=AB·sin∠B=4×sin60°=![]() ,
,
∴S△ABC=![]() AD·BC=
AD·BC=![]() .
.
故选D.
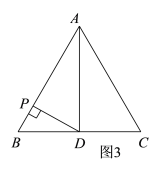
-
科目: 来源: 题型:
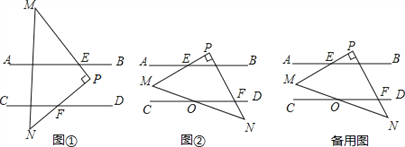
查看答案和解析>>【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A1, A2, A3, A4和C1, C2, C3, C4分别是AB和CD的五等分点,点B1, B2和D1,D2分别是BC和DA的三等分点.已知四边形A4B2C4D2的面积为18,则平行四边形ABCD的面积为( )
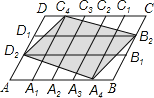
A. 22B. 25C. 30D. 15
-
科目: 来源: 题型:
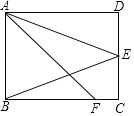
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E是CD的中点,点F是BC边上的点,AF=AD+FC,平行四边形ABCD的面积为S,由A、E、F三点确定的圆的周长为t.
(1)若△ABE的面积为30,直接写出S的值;
(2)求证:AE平分∠DAF;
(3)若AE=BE,AB=4,AD=5,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,⊙P的圆心是(2,a)(a >0),半径是2,与y轴相切于点C,直线y=x被⊙P截得的弦AB的长为
 ,则a的值是( )
,则a的值是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
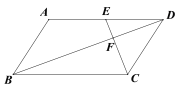
查看答案和解析>>【题目】如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF =3,则S□ABCD =_______.
-
科目: 来源: 题型:
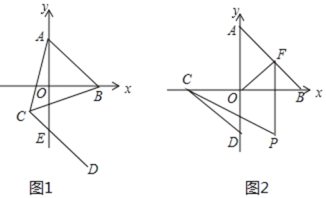
查看答案和解析>>【题目】.如图 1,在平面直角坐标系中,A 、B 在坐标轴上,其中 A(0, a) ,B(b, 0)满足| a 3 |
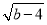 0.
0.(1)求 A 、 B 两点的坐标;
(2)将 AB 平移到CD , A 点对应点C(2, m) , DE 交 y 轴于 E ,若ABC 的面积等于13,求点 E 的坐标;
(3)如图 2,若将 AB 平移到CD ,点 C、D 也在坐标轴上,F 为线段 AB 上一动点,(不包括点 A ,点B) ,连接OF 、FP 平分BFO ,BCP 2PCD,试探究COF,OFP ,CPF 的数量关系.
相关试题

