Question

【题目】如图，在平面直角坐标系xOy中，⊙P的圆心是（2，a）（a >0），半径是2，与y轴相切于点C，直线y=x被⊙P截得的弦AB的长为，则a的值是（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】试题分析：过P点作PE⊥AB于E，连接PA并延长PA交x轴于点C．

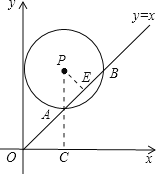
∵PE⊥AB，AB=2∴AE=AB=1，

∵PA=，

在Rt△PAE中，由勾股定理得：PE=1，

∴PE=AE，∴∠PAE=45°，

∵函数y=x的图象与y轴的夹角为45°，

∴y轴∥PA，∴∠PCO=90°，

∴A点的横坐标为，

∵A点在直线y=x上，

∴A点的纵坐标为，

∴PC=2，

∴a=2.

故选A.

考点: 1.切线的判定；2.一次函数图象上点的坐标特征；3.勾股定理；4.垂径定理．