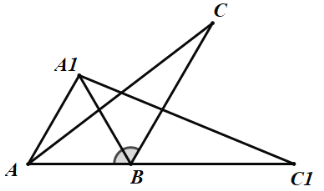
【题目】如图1，在△ABC中，∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于点A1，
（1）分别计算：当∠A分别为700、800时，求∠A1的度数.
（2）根据（1）中的计算结果，写出∠A与∠A1之间的数量关系___________________.
（3）∠A1BC的角平分线与∠A1CD的角平分线交于点A2，∠A2BC的角平分线与∠A2CD的角平分线交于点A3，如此继续下去可得A4，…，∠An，请写出∠A5与∠A的数量关系_________________.
（4）如图2，若E为BA延长线上一动点，连EC，∠AEC与∠ACE的角平分线交于Q，当E滑动时，有下面两个结论：①∠Q+∠A1的值为定值；②∠D-∠A1的值为定值.
其中有且只有一个是正确的，请写出正确的结论，并求出其值.
【答案】（1）∠A1=350 和∠A1=400;（2）∠A=2∠A1;（3）∠A5=
∠A;（4）①的结论是正确的，∠Q+∠A1=1800
【解析】
（1）由三角形的外角性质易知：∠A=∠ACD-∠ABC，∠A1=∠A1CD-∠A1BC，而∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1，可得∠A1=
（∠ACD-∠ABC）=∠A
（2）根据（1）可得到∠A=2∠A1
（3）根据（1）可得到∠A2=∠A1=
∠A，∠A3=∠A2=
∠A，…依此类推，∠An=
∠A，根据这个规律即可解题.
（4）用三角形的外角性质求解，易知2∠A1=∠AEC+∠ACE=2（∠QEC+∠QCE），利用三角形内角和定理表示出∠QEC+∠QCE，即可得到∠A1和∠Q的关系．
解：（1）∵A1C、A1B分别是∠ACD、∠ABC的角平分线
∴∠A1BC= ∠ABC，∠A1CD=∠ACD
由三角形的外角性质知：∠A=∠ACD-∠ABC，∠A1=∠A1CD-∠A1BC，即：
∠A1=（∠ACD-∠ABC）=∠A；
当∠A=70°时，∠A1=35°；当∠A=80°，∠A1=40°．
（2）由（1）可知∠A1==∠A
即∠A=2∠A1
（3）同（1）可求得：
∠A2=∠A1=∠A，
∠A3=∠A2=∠A，
…
依此类推，∠An=∠A；
当n=5时，∠A5=
∠A=∠A
（4）△ABC中，由三角形的外角性质知：∠BAC=∠AEC+∠ACE=2（∠QEC+∠QCE）；
即：2∠A1=2（180°-∠Q），
化简得：∠A1+∠Q=180°
故①的结论是正确的，且这个定值为180°.
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，矩形
的边
的边分别在
轴，
轴正半轴上，
， 点
从点
出发以每秒2个单位长度的速度向终点
运动，点不与点重合以
为边在
上方作正方形
，设正方形与
的重叠部分图形的面积为
（平方单位），点的运动时间为
（秒）．
（1）直线
所在直线的解析式是__________________________．
（2）当点
落在线段上时，求的值．
（3）在点运动的过程中，求与之间的函数关系式；
（4）设边的中点为
，点关于点的对称点为
，以
为边在上方作正方形
当正方形与
重叠部分图形为三角形时，直接写出的取值范围．
（提示：根据点的运动，可在草纸上画出正方形与重叠部分图形为不同图形时的临界状态去研究．）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，点
从点
出发沿
方向以
的速度向点
匀速运动，同时点
从点出发沿
方向以
的速度向点
匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点
运动的时间是
.过点作
于点
连结
（1）求证：
；
（2）四边形
能够成为菱形吗？如果能，求出相应的
值，如果不能，说明理由；
（3）当为何值时，
为直角三角形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在⊙O中，AB是⊙O的直径，AB＝10，
，点E是点D关于AB的对称点，M是AB上的一动点，下列结论：①∠BOE＝60°；②∠CED＝
∠DOB；③DM⊥CE；④CM＋DM的最小值是10，上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为美化市容市貌，我市在春节前夕计划在市区几个公园建造
、
两种型号花灯供市民观赏，根据预算，共需资金
万元．若建造一个种花灯和两个类种花灯共 需资金
万元；建造两个种花灯和一个种花灯共需资金
万元．
(1)问建造一个种型号花灯和一个种型号花灯所需资金分别是多少万元？
(2)若建造种型号花灯不超过
个，则种型号花灯至少要建造多少个？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】推理填空:已知如图，DG⊥BC于G，AC⊥BC于C，FE⊥AB于E，∠1=∠2，请说明CD⊥AB的理由:
解:∵DG⊥BC，AC⊥BC(已知)
∴∠DGC=∠ACB=90°(垂直定义
∴∠DGC+∠ACB=180°
∴DG∥AC(_________________________)
∴∠2=∠DCA(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠______=∠_____(等量代换)
∴EF∥CD(_____________________)
∴∠AEF=∠ADC(___________________)
∴FE⊥AB(已知)
∴AEF=90°(垂直定义)
∴∠ADC=90°
∴CD⊥AB(垂直定义)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
