搜索
【题目】如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．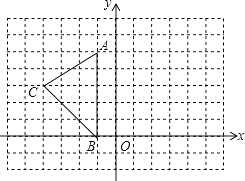 
（1）请画出△ABC关于y轴对称的△DEF（其中D，E，F分别是A，B，C的对应点，不写画法）；
（2）直接写出D，E，F三点的坐标：D（），E（），F（）；
（3）在y轴上存在一点，使PC﹣PB最大，则点P的坐标为 ．
参考答案：
【答案】
（1）解：如图，△DEF即为所求作三角形；
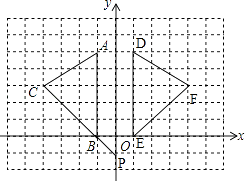
（2）1，5；1，0；4，3
（3）（0，﹣1）
【解析】解：（2）由图可知点D（1，5）、E（1，0）、F（4，3），
所以答案是：1，5；1，0；4，3；（3）延长CB交y轴于P，此时PC﹣PB最大，故点P即为所求，
设BC所在直线解析式为y=kx+b，
将点B（﹣1，0）、点C（﹣4，3）代入，得： 
，
解得： 
，
∴直线BC所在直线解析式为y=﹣x﹣1，
当x=0时，y=﹣1，
∴点P坐标为（0，﹣1），
所以答案是：（0，﹣1）．
【考点精析】关于本题考查的作轴对称图形和轴对称-最短路线问题，需要了解画对称轴图形的方法：①标出关键点②数方格，标出对称点③依次连线；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点E，F在BC上，BE=CF，∠A=∠D，∠B=∠C，AF与DE交于点O．
（1）求证：AB=DC；
（2）试判断△OEF的形状，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数
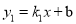与反比例函数
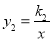的图象交于点
和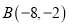
，与y轴交于点C.（1）m= ，
= ；（2）当x的取值是 时，
＞
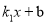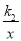；（3）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E，当
： 
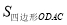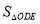=3:1时，求点P的坐标.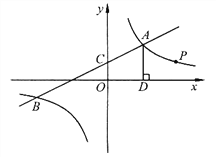
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知
的三个顶点的坐标分别为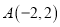
、
、
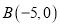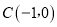，P（a，b）是△ABC的边AC上一点：（1）将
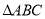绕原点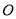
逆时针旋转90°得到
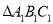,请在网格中画出
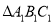，旋转过程中点A所走的路径长为 .（2）将△ABC沿一定的方向平移后，点P的对应点为P2（a+6，b+2），请在网格画出上述平移后的△A2B2C2，并写出点A2、的坐标:A2（ ）.
（3）若以点O为位似中心，作△A3B3C3与△ABC成2:1的位似，则与点P对应的点P3位似坐标为 （直接写出结果).
-
科目： 来源： 题型：
查看答案和解析>>【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图：
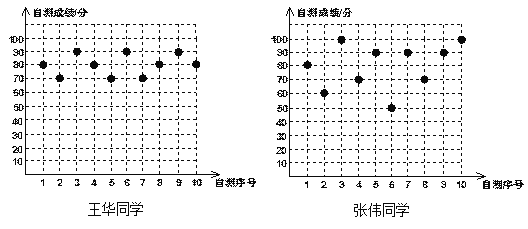
（1）根据上图中提供的数据列出如下统计表：
平均成绩（分）
中位数（分）
众数（分）
方差（S2）
王华
80
b
80
d
张伟
a
85
c
260
则a= ，b= ，c= ，d= ，
（2）将90分以上（含90分）的成绩视为优秀，则优秀率高的是 .
（3）现在要从这两个同学选一位去参加数学竞赛，你可以根据以上的数据给老师哪些建议？
-
科目： 来源： 题型：
查看答案和解析>>【题目】若关于x的方程x2+3x+a=0有一个根为﹣1，则a的值为（ ）
A.2
B.﹣1
C.﹣2
D.1 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，分别得到点A，B的对应点C，D，连接AC，BD，CD.
(1)求点C，D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q，连接QA，QB，使S△QAB＝S四边形ABDC？若存在这样一点，求出点Q的坐标；若不存在，试说明理由．
(3)如图②，点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时(不与B，D重合)，给出下列结论：①
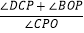的值不变，②
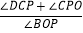的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．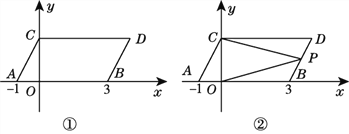
相关试题
