【题目】如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O. 
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
参考答案:
【答案】
(1)证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE.
又∵∠A=∠D,∠B=∠C,
∴△ABF≌△DCE(AAS),
∴AB=DC
(2)解:△OEF为等腰三角形
理由如下:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∴△OEF为等腰三角形
【解析】(1)根据BE=CF得到BF=CE,又∠A=∠D,∠B=∠C,所以△ABF≌△DCE,根据全等三角形对应边相等即可得证;(2)根据三角形全等得∠AFB=∠DEC,所以是等腰三角形.
【考点精析】关于本题考查的等腰三角形的判定,需要了解如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
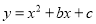 的顶点为P,与y轴交于点A,与直线OP交于点B.
的顶点为P,与y轴交于点A,与直线OP交于点B.(1)如图1,若点P的横坐标为1,点
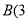 ,
, 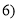 ,试确定抛物线的解析式;
,试确定抛物线的解析式;(2)在(1)的条件下,若点M是直线AB下方抛物线上的一点,且S△ABM=3,求点M的坐标;
(3)如图2,若P在第一象限,且
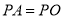 ,过点P作
,过点P作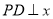 轴于点D,将抛物线
轴于点D,将抛物线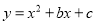 平移,平移后的抛物线经过点A、D,该抛物线与
平移,平移后的抛物线经过点A、D,该抛物线与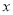 轴的另一个交点为C,请探索四边形OABC的形状,并说明理由.
轴的另一个交点为C,请探索四边形OABC的形状,并说明理由.
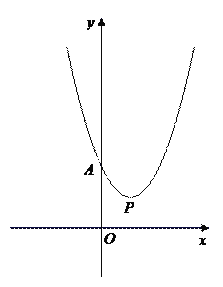
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(a3)2a2的结果是( )
A.a7
B.a8
C.a10
D.a11 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x5+x5=x10
B.(x3)3=x6
C.x3x2=x5
D.x6﹣x3=x3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
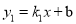 与反比例函数
与反比例函数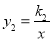 的图象交于点
的图象交于点 和
和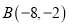 ,与y轴交于点C.
,与y轴交于点C.(1)m= ,
 = ;
= ;(2)当x的取值是 时,
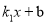 >
>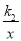 ;
;(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当
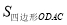 :
: 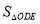 =3:1时,求点P的坐标.
=3:1时,求点P的坐标.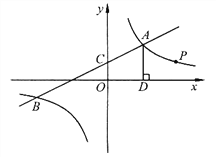
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 的三个顶点的坐标分别为
的三个顶点的坐标分别为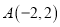 、
、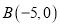 、
、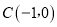 ,P(a,b)是△ABC的边AC上一点:
,P(a,b)是△ABC的边AC上一点:(1)将
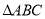 绕原点
绕原点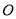 逆时针旋转90°得到
逆时针旋转90°得到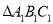 ,请在网格中画出
,请在网格中画出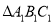 ,旋转过程中点A所走的路径长为 .
,旋转过程中点A所走的路径长为 .(2)将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2,并写出点A2、的坐标:A2( ).
(3)若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为 (直接写出结果).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
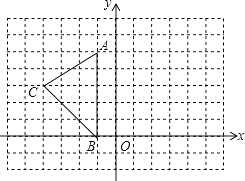
(1)请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);
(2)直接写出D,E,F三点的坐标:D(),E(),F();
(3)在y轴上存在一点,使PC﹣PB最大,则点P的坐标为 .
相关试题

