【题目】函数y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0),(m,0),且1<m<2,当x<﹣1时,y随x增大而减小,下列结论: ①abc>0;
②a+b<0;
③若点A(﹣3,y1),B(3,y2)在抛物线上,则y1<y2;
④a(m﹣1)+b=0;
⑤c≤﹣1时,则b2﹣4ac≤4a.
其中结论正确的有 .
参考答案:
【答案】①④
【解析】解:如图, 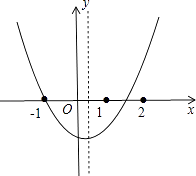
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,
所以①的结论正确;
∵抛物线过点(﹣1,0)和(m,0),且1<m<2,
∴0<﹣ ![]() <
< ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() >0,
>0,
∴a+b>0,
所以②的结论错误;
∵点A(﹣3,y1)到对称轴的距离比点B(3,y2)到对称轴的距离远,
∴y1>y2 ,
所以③的结论错误;
∵抛物线过点(﹣1,0),(m,0),
∴a﹣b+c=0,am2+bm+c=0,
∴am2﹣a+bm+b=0,
a(m+1)(m﹣1)+b(m+1)=0,
∴a(m﹣1)+b=0,
所以④的结论正确;
∵ ![]() <c,
<c,
而c≤﹣1,
∴ ![]() <﹣1,
<﹣1,
∴b2﹣4ac>4a,所以⑤的结论错误.
所以答案是①④.
【考点精析】掌握二次函数图象以及系数a、b、c的关系是解答本题的根本,需要知道二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.

(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个锐角的和等于90°,那么我们就称这两个角互为余角.类似可以定义:如果两个角的差的绝对值等于90°,那么我们就可以称这两个角互为垂角.例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角).
(1)如图,O为直线AB上一点,OC⊥AB于点O,OE⊥OD于点O ,请写出图中所有互为垂角的角:_______________________________________________________;
(2)如果一个角的垂角等于这个角的补角的
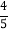 ,求这个角的度数.
,求这个角的度数.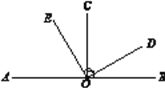
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数-5,1,-3,5,-2中任取三个数相乘,其中最大的积是a,最小的积是b.
(1)求a,b的值;
(2)若|x+a|+|y-b|=0,求(x+y)÷(x-y)的值.
-
科目: 来源: 题型:
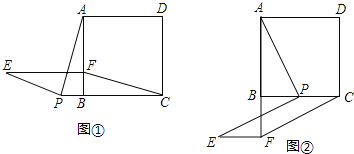
查看答案和解析>>【题目】如图,正方形ABCD中,点P是直线BC上一点,连接PA,将线段PA绕 点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF、CF.
(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形.
(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划购买A、B两种品牌的显示器共120台,A、B两种品牌显示器的单价分别为800元和1000元,设购买A品牌显示器x台,若学校购买这两种品牌显示器的总费用为110000元,那么A、B两种品牌的显示器各购买了多少台?根据题目信息完成上面的表格,并列出方程,列出的方程: .
项目品牌
单价/元
购买数量/台
购买费用/元
A
800
x
B
1000
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 )﹣2+(
)﹣2+( 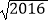 ﹣
﹣ 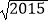 )0+|
)0+| 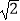 ﹣1|+(
﹣1|+( 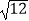 ﹣3
﹣3 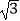 )tan60°.
)tan60°.
相关试题

