搜索
【题目】某学校计划购买A、B两种品牌的显示器共120台，A、B两种品牌显示器的单价分别为800元和1000元，设购买A品牌显示器x台，若学校购买这两种品牌显示器的总费用为110000元，那么A、B两种品牌的显示器各购买了多少台？根据题目信息完成上面的表格，并列出方程，列出的方程： ．
项目品牌 | 单价/元 | 购买数量/台 | 购买费用/元 |
A | 800 | x |
|
B | 1000 |
|
|
参考答案：
【答案】800x+1000（120﹣x）=110000
【解析】根据题意，设购买A品牌显示器x台，需要800x元，
则购买B品显示器(120x)台,需要费用1000(120x)元，
完成表格如下：
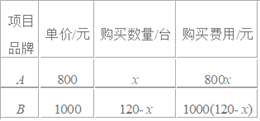
列出的方程：800x+1000(120x)=110000，
故答案为：800x+1000(120x)=110000.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=ax2+bx（a≠0）的图象经过点A（1，4），对称轴是直线x=﹣
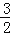，线段AD平行于x轴，交抛物线于点D．在y轴上取一点C（0，2），直线AC交抛物线于点B，连结OA，OB，OD，BD．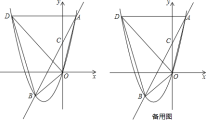
（1）求该二次函数的解析式；
（2）求点B坐标和坐标平面内使△EOD∽△AOB的点E的坐标；
（3）设点F是BD的中点，点P是线段DO上的动点，问PD为何值时，将△BPF沿边PF翻折，使△BPF与△DPF重叠部分的面积是△BDP的面积的
？ -
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式-4a3+8a2-4a = _____ _ ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为增强公民节水意识，合理利用水资源，某市采用“阶梯收费”，标准如下表：
用水量
单价
不超过6m3 的部分
2元/ m3
超过6m3不超过10m3的部分
4元/m3
超出10m3的部分
8元/m3
譬如：某用户2月份用水9m3，则应缴水费：2×6+4×(9－6)=24(元)
(1)某用户3月用水15 m3应缴水费多少元？
(2) 已知某用户4月份缴水费20元，求该用户4月份的用水量；
(3) 如果该用户5、6月份共用水20m3 （6月份用水量超过5月份用水量），共交水费64元，则该户居民5、6月份各用水多少立方米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线l1的函数解析式为y=﹣2x+4，且l1与x轴交于点D，直线l2经过点A、B，直线l1、l2交于点C．
（1）求直线l2的函数解析式；
（2）求△ADC的面积；
（3）在直线l2上是否存在点P，使得△ADP面积是△ADC面积的2倍？如果存在，请求出P坐标；如果不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简再求值：（2a-b）2-2（a+1）（a-2b），其a=2，b=-1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A从原点出发沿数轴向左运动，同时，点B也从原点出发沿数轴向右运动，4秒后，两点相距16个单位长度．已知点B的速度是点A的速度的3倍（速度单位：单位长度/秒）．
（1）求出点A、点B运动的速度，并在数轴上标出A、B两点从原点出发运动4秒时的位置；
（2）若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动，再过几秒时，原点恰好处在AB的中点？
（3）若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动时，另一点C同时从原点O位置出发向B点运动，且C的速度是点A的速度的一半；当点C运动几秒时，C为AB的中点？
相关试题
