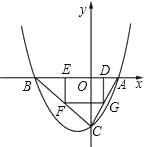
【题目】如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
x | … | ﹣3 | ﹣2 | 1 | 2 | … |
y | … |
| ﹣4 |
| 0 | … |
(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF,若点M不在抛物线P上,求k的取值范围.
参考答案:
【答案】(1)A(2,0),B(﹣4,0),C(0,﹣4);(2)SDEFG=12m﹣6m2(0<m<2);(3)k≠![]() 且k>0.
且k>0.
【解析】
试题分析:(1)根据图表可以得到,抛物线经过的四点的坐标,根据待定系数法,设y=ax2+bx+c,把其中三点的坐标代入,就可以求得函数解析式.进而可以求出A、B、C的坐标;(2)表示出矩形的长和宽是解决问题的关键,先证△ADG∽△AOC,AD=2﹣m,根据相似三角形的对应边的比相等,就可以用m表示出DG的长,再根据△BEF∽△BOC,就可以表示出BE,进而得到OE,于是ED就可以表示出来.因而S与m的函数关系就可以得到;(3)当矩形DEFG的面积S取最大值时,就是函数的值是最大值时,根据二次函数的性质就可以求出相应的m的值.则矩形的四个顶点的坐标就可以求出,根据待定系数法就可以求出直线DF的解析式.可以求出直线DF与抛物线的交点的坐标,根据FM=kDF,就可以表示出M的坐标,把M的坐标代入函数就可以得到一个关于k的方程,求出k的值,判断是否满足函数的解析式即可.
试题解析:(1)根据待定系数法,设y=ax2+bx+c(a≠0),任取x,y的三组值代入,求出解析式为y=![]() x2+x﹣4,令y=0,求出x1=﹣4,x2=2;令x=0,得y=﹣4,∴A、B、C三点的坐标分别是A(2,0),B(﹣4,0),C(0,﹣4).(2)由题意,△ADG∽△AOC,所以
x2+x﹣4,令y=0,求出x1=﹣4,x2=2;令x=0,得y=﹣4,∴A、B、C三点的坐标分别是A(2,0),B(﹣4,0),C(0,﹣4).(2)由题意,△ADG∽△AOC,所以![]() ,而AO=2,OC=4,AD=2﹣m,故DG=4﹣2m,又△BEF∽△BOC,所以
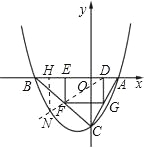
,而AO=2,OC=4,AD=2﹣m,故DG=4﹣2m,又△BEF∽△BOC,所以![]() ,EF=DG,得BE=4﹣2m,∴DE=3m,∴SDEFG=DGDE=(4﹣2m)3m=12m﹣6m2(0<m<2),故S=12m﹣6m2(0<m<2);(3)如下图,连接DF并延长,∵SDEFG=12m﹣6m2(0<m<2),∴m=1时,矩形的面积最大,且最大面积是6.当矩形面积最大时,其顶点为D(1,0),G(1,﹣2),F(﹣2,﹣2),E(﹣2,0),设直线DF的解析式为y=kx+b,易知,k=
,EF=DG,得BE=4﹣2m,∴DE=3m,∴SDEFG=DGDE=(4﹣2m)3m=12m﹣6m2(0<m<2),故S=12m﹣6m2(0<m<2);(3)如下图,连接DF并延长,∵SDEFG=12m﹣6m2(0<m<2),∴m=1时,矩形的面积最大,且最大面积是6.当矩形面积最大时,其顶点为D(1,0),G(1,﹣2),F(﹣2,﹣2),E(﹣2,0),设直线DF的解析式为y=kx+b,易知,k=![]() ,b=﹣
,b=﹣![]() ,∴y=
,∴y=![]() x﹣
x﹣![]() ,又可求得抛物线P的解析式为:y=
,又可求得抛物线P的解析式为:y=![]() x2+x﹣4,令
x2+x﹣4,令![]() x﹣
x﹣![]() =
=![]() x2+x﹣4,可求出x=
x2+x﹣4,可求出x=![]() .设射线DF与抛物线P相交于点N,则N的横坐标为
.设射线DF与抛物线P相交于点N,则N的横坐标为![]() ,过N作x轴的垂线交x轴于H,有
,过N作x轴的垂线交x轴于H,有![]() =
=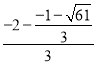 =
=![]() ,点M不在抛物线P上,即点M不与N重合时,此时k的取值范围是k≠
,点M不在抛物线P上,即点M不与N重合时,此时k的取值范围是k≠![]() 且k>0.
且k>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从标号分别为1,2,3,4,5的5张卡片中,随机抽取一张,下列事件中,必然事件是( )
A.标号小于6 B.标号大于6 C.标号是奇数 D.标号是3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果规定收入为正,支出为负.收入500 元记作500元,那么支出237元应记作 ( )
A. ﹣500元 B. ﹣237元 C. 237元 D. 50
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2是方程x2﹣2x+a=0的两个实数根,且x1+2x2=3﹣
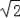 .
.(1)求x1,x2及a的值;
(2)求x13﹣3x12+2x1+x2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣4b=﹣18,b2+10c=7,c2﹣6a=﹣27,则a+b+c的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林活动.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
植树数量(单位:棵)
4
5
6
8
10
人数
30
22
25
15
8
则这100名同学平均每人植树棵;若该校共有1000名学生,请根据以上调查结果估计该校学生的植树总数是棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:(1)x2y﹣4y;
(2)(a+2)(a﹣2)+3a.
相关试题

