Question

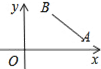
【题目】如图，在直角坐标系中有线段AB，AB＝50cm，A、B到x轴的距离分别为10cm和40cm，B点到y轴的距离为30cm，现在在x轴、y轴上分别有动点P、Q，当四边形PABQ的周长最短时，则这个值为（　　）

A. 50 B. 50 C. 50－50 D. 50＋50

Answer 1

【答案】D

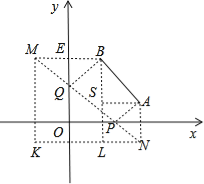
【解析】试题分析：过B点作BM⊥y轴交y轴于E点，截取EM=BE，过A点作AN⊥x轴交x轴于F点，截取NF=AF，连接MN交X，Y轴分别为P，Q点，此时四边形PABQ的周长最短，根据题目所给的条件可求出周长．

解：过B点作BM⊥y轴交y轴于E点，截取EM=BE，过A点作AN⊥x轴交x轴于F点，截取NF=AF，连接MN交x，y轴分别为P，Q点，

过M点作MK⊥x轴，过N点作NK⊥y轴，两线交于K点．

MK=40+10=50，

作BL⊥x轴交KN于L点，过A点作AS⊥BP交BP于S点．

∵LN=AS==40．

∴KN=60+40=100．

∴MN==50．

∵MN=MQ+QP+PN=BQ+QP+AP=50．

∴四边形PABQ的周长=50+50．

故选D．