【题目】如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 . 
参考答案:
【答案】![]()
【解析】解:作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点. 此时PA+PB最小,且等于AC的长.
连接OA,OC,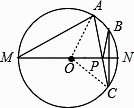
∵∠AMN=30°,
∴∠AON=60°,
∴弧AN的度数是60°,
则弧BN的度数是30°,
根据垂径定理得弧CN的度数是30°,
则∠AOC=90°,又OA=OC=1,
则AC= ![]() .
.
首先利用在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点P的位置,然后根据弧的度数发现一个等腰直角三角形计算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)分解因式:
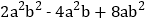 (2)分解因式: 9a2(x—y)+4b2(y—x)
(2)分解因式: 9a2(x—y)+4b2(y—x) (3)分解因式:(x2+y2)2-4x2y2 (4)利用分解因式计算求值:2662-2342
(5)利用分解因式计算求值:已知x-3y=-1,xy=2,求x3y-6x2y2+9xy3的值.
-
科目: 来源: 题型:
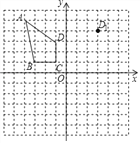
查看答案和解析>>【题目】如图所示,在网格中建立平面直角坐标系,每个小正方形的边长都是1个单位长度,四边形ABCD的各顶点均在网格点上.
(1)将四边形ABCD平移,使得D点平移到D1(3,4),画出平移后的四边形A1B1C1D1;
(2)画出四边形ABCD绕着原点O逆时针旋转90°后的四边形A2B2C2D2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=
 x的图像如图所示,则方程ax2+(b﹣
x的图像如图所示,则方程ax2+(b﹣  )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( ) 
A.大于0
B.等于0
C.小于0
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=
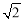 ,求AD的长.
,求AD的长.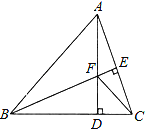
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b互为相反数,b、C互为倒数,并且m的立方等于它本身
(1)求
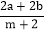 +ac值;
+ac值;(2)若a>1,且m<0,S=|2a-3b|-2|b-m|-|b+
 |,求2a-S的值.
|,求2a-S的值.(3)若m≠0,试讨论:x为有理数时|x+m|-|x-m|是否存在最大值?若存在,求出这个最大值:若不存在,请说明理由.
-
科目: 来源: 题型:
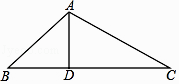
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
相关试题

