【题目】如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长. 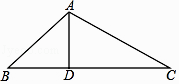
参考答案:
【答案】解:∵AD⊥BC, ∴∠ADB=∠ADC=90°.
在Rt△ADB中,
∵∠B+∠BAD=90°,∠B=45°,
∴∠B=∠BAD=45°,
∴AD=BD=1,AB= ![]() .
.
在Rt△ADC中,
∵∠C=30°,
∴AC=2AD=2,
∴CD= ![]() ,BC=BD+CD=1+
,BC=BD+CD=1+ ![]() ,
,
∴AD+AC+BC= ![]() +
+ ![]() +3
+3
【解析】先根据题意得出AAD=BD,再由勾股定理得出AB的长,在Rt△ADC中,根据直角三角形的性质得出AC及CD的长,进而可得出结论.
【考点精析】通过灵活运用勾股定理的概念,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=
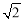 ,求AD的长.
,求AD的长.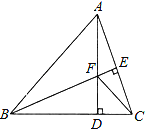
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b互为相反数,b、C互为倒数,并且m的立方等于它本身
(1)求
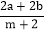 +ac值;
+ac值;(2)若a>1,且m<0,S=|2a-3b|-2|b-m|-|b+
 |,求2a-S的值.
|,求2a-S的值.(3)若m≠0,试讨论:x为有理数时|x+m|-|x-m|是否存在最大值?若存在,求出这个最大值:若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+2与双曲线y=
x+2与双曲线y=  相交于点A(m,3),与x轴交于点C.
相交于点A(m,3),与x轴交于点C. 
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4,如图2,正方形ABCD顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长. 例如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D,若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B,…设游戏者从圈A起跳.

(1)若随机掷一次骰子,求落回到圈A的概率P1;
(2)若随机掷两次骰子,用列表法或树状图法求出最后落回到圈A的概率P. -
科目: 来源: 题型:
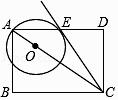
查看答案和解析>>【题目】如图,在矩形ABCD中,点O在对角线AB上,以OA的长为半径的圆O与AD交于点E,且∠ACB=∠DCE,求证:CE是⊙O的切线.
相关试题

