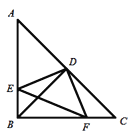
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是AC的中点,直角
,点D是AC的中点,直角![]() 的两边分别交AB、BC于点E、F,给出以下结论:①
的两边分别交AB、BC于点E、F,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 是等腰直角三角形. 当
是等腰直角三角形. 当![]() 在
在![]() 内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.
内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.
参考答案:
【答案】4
【解析】
由ED垂直于FD,BD垂直于AC,利用同角的余角相等得到一对角相等,再由三角形ABC为等腰直角三角形得到BD=CD,且∠EBD=∠C=45°,利用ASA得到三角形BED与三角形CFD全等,利用全等三角形的对应边相等,对应角相等即可做出判断.
∵ED⊥FD,BD⊥AC,
∴∠BDE+∠BDF=90°,∠BDF+∠FDC=90°,
∴∠BDE=∠FDC,
∵B、E、D、F四点共圆,
∴∠BFE=∠BDE,
∴∠BFE=∠CDF,选项④正确;
∵△ABC为等腰直角三角形,BD⊥AC,
∴∠EBD=∠C=45°,BD=CD,
在△BED和△CFD中,
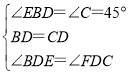 ,
,
∴△BED≌△CFD(ASA),
∴BE=CF,
∴AE=BF,选项①正确;
DE=DF,
∴△DEF为等腰直角三角形,选项⑤正确;
∴S四边形BEDF=S△BED+S△BDF=S△CFD+S△BDF=S△BDC=![]() S△ABC,选项②正确.
S△ABC,选项②正确.
∵BD是定值,EF随DF的变化而变化,只有当DF⊥BC时,EF=BD,
∴③不正确,
∴上述结论中始终成立的有4个.
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,点
,点 、
、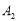 、
、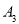 、…在射线ON上,点
、…在射线ON上,点 、
、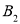 、
、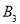 、…在射线OM上,
、…在射线OM上, 、
、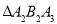 、
、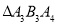 …均为等边三角形,若
…均为等边三角形,若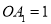 ,则
,则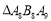 的边长为( )
的边长为( )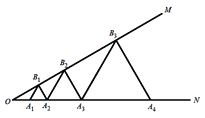
A.16B.64C.128D.256
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD
(1)求证:CD是⊙O的切线;
(2)如图2,连AC交BD于E.若AE=CE,求tan∠ACB的值.
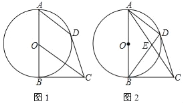
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别是x轴、y轴上的点,点A的坐标为(a,0),点B的坐标为(0,b),点M坐标为(1,1)
(1)如图1中的第一象限内,若a=2,b=1,画出线段AB关于点M(1,1)的中心对称线段CD,并写出C、D两点的坐标;
(2)如图,若AB关于M(1,1)中心对称的线段为CD,点C、点D在双曲线y=
 (x>0)上,且AB=
(x>0)上,且AB= ,求k的值;
,求k的值;(3)若a=
 ,b=
,b= ,直接写出直线CD的解析式.
,直接写出直线CD的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
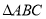 三个顶点的坐标分别为
三个顶点的坐标分别为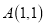 、
、 、
、 .
.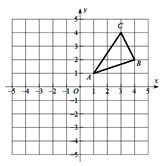
(1)若
 与
与 关于y轴成轴对称,则
关于y轴成轴对称,则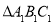 三个顶点坐标分别为
三个顶点坐标分别为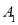 _________,
_________,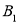 ____________,
____________,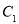 ____________;
____________;(2)若P为x轴上一点,则
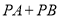 的最小值为____________;
的最小值为____________;(3)计算
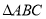 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,BC>AC,CD平分∠ACB交于AB于D,E,F分别是AC,BC边上的两点,EF交于CD于H,
(1)如图1,若∠EFC=∠A,求证:CECD=CHBC;
(2)如图2,若BH平分∠ABC,CE=CF,BF=3,AE=2,求EF的长;
(3)如图3,若CE≠CF,∠CEF=∠B,∠ACB=60°,CH=5,CE=4
 ,求
,求 的值.
的值.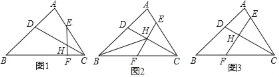
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了积极响应国家新农村建设,某市镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路
 的一侧点
的一侧点 处有一村庄,村庄
处有一村庄,村庄 到公路
到公路 的距离为800米,假使宣讲车
的距离为800米,假使宣讲车 周围1000米以内能听到广播宣传,宣讲车
周围1000米以内能听到广播宣传,宣讲车 在公路
在公路 上沿
上沿 方向行驶时:
方向行驶时:
(1)请问村庄能否听到宣传,并说明理由;
(2)如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?
相关试题

