【题目】如图,点A、B分别是x轴、y轴上的点,点A的坐标为(a,0),点B的坐标为(0,b),点M坐标为(1,1)
(1)如图1中的第一象限内,若a=2,b=1,画出线段AB关于点M(1,1)的中心对称线段CD,并写出C、D两点的坐标;
(2)如图,若AB关于M(1,1)中心对称的线段为CD,点C、点D在双曲线y=![]() (x>0)上,且AB=
(x>0)上,且AB=![]() ,求k的值;
,求k的值;
(3)若a=![]() ,b=
,b=![]() ,直接写出直线CD的解析式.
,直接写出直线CD的解析式.

参考答案:
【答案】(1)C(0,1),D(2,1);(2)k=2;(3)y=﹣x+![]() .
.
【解析】
(1)如图1中,设C(m,n),D(p,q).利用中点坐标公式计算即可;
(2)如图2中,由题意点C的纵坐标为2,点D的横坐标为2,由点C、D在反比例函数y=![]() 上,可以假设C(m,2),D(2,m),根据AB=CD=
上,可以假设C(m,2),D(2,m),根据AB=CD=![]() ,2-m=1,可得m=1,求出点D坐标即可解决问题;
,2-m=1,可得m=1,求出点D坐标即可解决问题;
(3)设C(m,n),D(p,q).利用中点坐标公式求出C、D两点坐标,再利用待定系数法即可解决问题;
解:(1)如图1中,设C(m,n),D(p,q).

由题意A(2,0),B(0,1),
∵A、C关于M对称,B、D关于M对称,
∴![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,
解得m=0,n=2,p=2,q=1,
∴C(0,1),D(2,1).
(2)如图2中,由题意点C的纵坐标为2,点D的横坐标为2,

∵点C、D在反比例函数y=![]() 上,
上,
∴可以假设C(m,2),D(2,m),
∵AB=CD=![]() ,
,
∴2﹣m=1,
∴m=1,
∴C(1,2),D(2,1),
把C(1,2)代入y=![]() 中,得到k=2.
中,得到k=2.
(3)设C(m,n),D(p,q).由题意A(![]() ,0),B(0,
,0),B(0,![]() ),
),
∵A、C关于M对称,B、D关于M对称,
∴![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,
解得m=![]() ,n=2,p=2,q=
,n=2,p=2,q=![]() ,
,
∴C(![]() ,2),D(2,
,2),D(2,![]() ),设直线CD的解析式为y=kx+b,
),设直线CD的解析式为y=kx+b,
则有 ,解得
,解得 ,
,
∴直线CD的解析式为y=﹣x+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区决定购置一批共享单车,经市场调查得知,购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需1600元.
(1)求男式单车和女式单车每辆分别是多少元?
(2)该社区要求男式单车比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过5000元,问该社区有几种购置方案?怎样的购置才能使所需总费用最低?最低费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
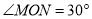 ,点
,点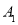 、
、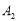 、
、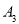 、…在射线ON上,点
、…在射线ON上,点 、
、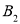 、
、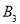 、…在射线OM上,
、…在射线OM上, 、
、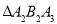 、
、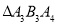 …均为等边三角形,若
…均为等边三角形,若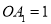 ,则
,则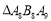 的边长为( )
的边长为( )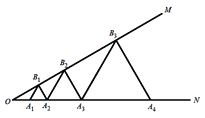
A.16B.64C.128D.256
-
科目: 来源: 题型:
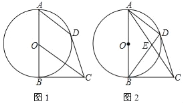
查看答案和解析>>【题目】如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD
(1)求证:CD是⊙O的切线;
(2)如图2,连AC交BD于E.若AE=CE,求tan∠ACB的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
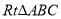 中,
中,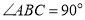 ,
,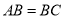 ,点D是AC的中点,直角
,点D是AC的中点,直角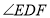 的两边分别交AB、BC于点E、F,给出以下结论:①
的两边分别交AB、BC于点E、F,给出以下结论:①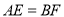 ;②
;②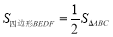 ;③
;③ ;④
;④ ;⑤
;⑤ 是等腰直角三角形. 当
是等腰直角三角形. 当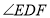 在
在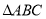 内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.
内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.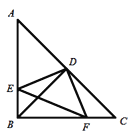
-
科目: 来源: 题型:
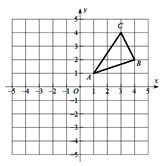
查看答案和解析>>【题目】如图,
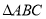 三个顶点的坐标分别为
三个顶点的坐标分别为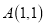 、
、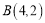 、
、 .
.
(1)若
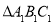 与
与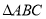 关于y轴成轴对称,则
关于y轴成轴对称,则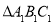 三个顶点坐标分别为
三个顶点坐标分别为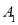 _________,
_________,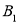 ____________,
____________,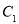 ____________;
____________;(2)若P为x轴上一点,则
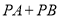 的最小值为____________;
的最小值为____________;(3)计算
 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,BC>AC,CD平分∠ACB交于AB于D,E,F分别是AC,BC边上的两点,EF交于CD于H,
(1)如图1,若∠EFC=∠A,求证:CECD=CHBC;
(2)如图2,若BH平分∠ABC,CE=CF,BF=3,AE=2,求EF的长;
(3)如图3,若CE≠CF,∠CEF=∠B,∠ACB=60°,CH=5,CE=4
 ,求
,求 的值.
的值.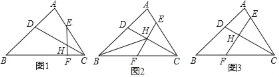
相关试题

