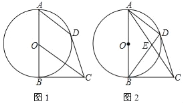
【题目】如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD
(1)求证:CD是⊙O的切线;
(2)如图2,连AC交BD于E.若AE=CE,求tan∠ACB的值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)欲证明CD是⊙O的切线,只要证明∠ODC=90°,只要证明△OCD≌△OCB即可.
(2)如图2中,连接OC交BD于点M,连接OE,设EM=a,BM=2a,利用△EOM∽△EBO,得EO2=EMEB,求出EO、EB即可解决问题.
(1)证明:如图1中,连接BD、OD,BD与OC交于点E.

∵AB是直径,
∴∠ADB=90°,
∴AD⊥BD,
∵AD∥OC,
∴OC⊥BD,ED=BE,
∵OD=OB,
∴∠DOC=∠BOC,
∵BC是⊙O切线,
∴OB⊥BC,
∴∠OBC=90°,
在△OCD和△OCB中,
 ,
,
∴△OCD≌△OCB,
∴∠ODC=∠OBC=90°,
∴OD⊥CD,
∴CD是⊙O切线.
(2)如图2中,连接OC交BD于点M,连接OE,

∵AO=OB,AE=EC,
∴OE∥BC,OE=![]() BC,
BC,
∴![]() ,设EM=a,BM=2a,∠AOE=∠ABC=90°,
,设EM=a,BM=2a,∠AOE=∠ABC=90°,
∵∠OEM=∠OEB,∠OME=∠EOB=90°,
∴△EOM∽△EBO,
∴EO2=EMEB=a3a
∴EO=![]() a,
a,
同理BO2=BMBE=6a2,
∴BO=AO=![]() a,
a,
∵∠AEO=∠ACB,
∴tan∠ACB=tan∠AEO=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目.为了解学生最喜爱哪一种项目,童威随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出)
(1)本次被调查的学生人数为 ,扇形统计图中“跑步”所对的圆心角为 度.
(2)补全条形统计图;
(3)该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区决定购置一批共享单车,经市场调查得知,购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需1600元.
(1)求男式单车和女式单车每辆分别是多少元?
(2)该社区要求男式单车比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过5000元,问该社区有几种购置方案?怎样的购置才能使所需总费用最低?最低费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
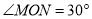 ,点
,点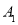 、
、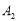 、
、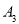 、…在射线ON上,点
、…在射线ON上,点 、
、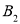 、
、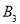 、…在射线OM上,
、…在射线OM上, 、
、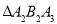 、
、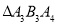 …均为等边三角形,若
…均为等边三角形,若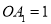 ,则
,则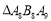 的边长为( )
的边长为( )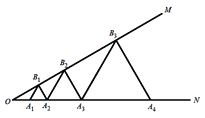
A.16B.64C.128D.256
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别是x轴、y轴上的点,点A的坐标为(a,0),点B的坐标为(0,b),点M坐标为(1,1)
(1)如图1中的第一象限内,若a=2,b=1,画出线段AB关于点M(1,1)的中心对称线段CD,并写出C、D两点的坐标;
(2)如图,若AB关于M(1,1)中心对称的线段为CD,点C、点D在双曲线y=
 (x>0)上,且AB=
(x>0)上,且AB= ,求k的值;
,求k的值;(3)若a=
 ,b=
,b= ,直接写出直线CD的解析式.
,直接写出直线CD的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
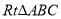 中,
中,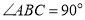 ,
,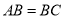 ,点D是AC的中点,直角
,点D是AC的中点,直角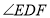 的两边分别交AB、BC于点E、F,给出以下结论:①
的两边分别交AB、BC于点E、F,给出以下结论:①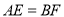 ;②
;②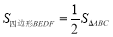 ;③
;③ ;④
;④ ;⑤
;⑤ 是等腰直角三角形. 当
是等腰直角三角形. 当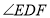 在
在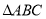 内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.
内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.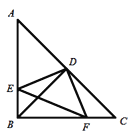
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
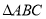 三个顶点的坐标分别为
三个顶点的坐标分别为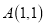 、
、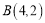 、
、 .
.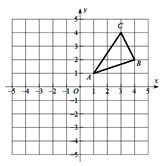
(1)若
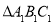 与
与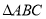 关于y轴成轴对称,则
关于y轴成轴对称,则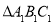 三个顶点坐标分别为
三个顶点坐标分别为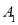 _________,
_________,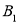 ____________,
____________,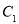 ____________;
____________;(2)若P为x轴上一点,则
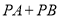 的最小值为____________;
的最小值为____________;(3)计算
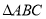 的面积.
的面积.
相关试题

