【题目】阅读材料:我们知道:如果点A.B在数轴上分别表示有理数a、b,那么A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|ab|.
根据上述材料,利用数轴解答下列问题:
![]()
(1)如果点A在数轴上表示2,将点A先向左平移2个单位长度,再向右移动7个单位长度,那么终点B在数轴上表示的数是___;
(2)数轴上表示x和1的两个点之间的距离是___;
(3)若|x3|+|x+2|=7,则x的值是___;
(4)在(1)的条件下,设点P在数轴上表示的数为x,当|PA||PB|=2时,则x的值是___.
参考答案:
【答案】(1)3;(2)|x-1|;(3)x=4或-3;(4)![]() ;
;
【解析】
(1)根据题意给出的定义即可求出答案.
(2)根据题意给出的定义即可求出答案.
(3)根据题意给出的定义即可求出答案.
(4)根据题意给出的定义即可求出答案.
(1)由题意可知:A=-2,
∴B=A-2+7=3
(2)由题意可知:|x-1|
(3)由题意可知:|x-3|表示数x与3的距离,
|x+2|表示数x与-2的距离,
而-2与3之间的距离为5,
故x必须在-2的左侧或3的右侧,
当x<-2时,
原方程化为:-(x-3)-(x+2)=7
解得:x=-3,满足题意;
当x>3时,
原方程化为:(x-3)+(x+2)=7
解得:x=4
综上所述,x=4或-3
(4)由|PA|-|PB|=2可知:点P必定在A的右侧,
∴当-2<x<3时,
∴|PA|=|x+2|=x+2
|PB=|x-3|=3-x
∴(x+2)-(3-x)=2
∴x+2-3+x=2
∴x=![]()
当x≥3时,
∴|PA|=|x+2|=x+2
|PB=|x-3|=x-3
∴(x+2)-(x-3)=2
∴5=2,不成立
综上所述,x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为等边三角形ABC内的一点, DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ABCD′=6+
 ,其中正确的有( )
,其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
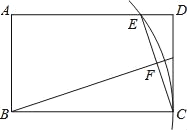
A.
 B.
B. 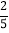 C.
C. 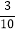 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场欲购进果汁饮料和碳酸饮料共60箱,两种饮料每箱的进价和售价如下表所示。设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注:总利润=总售价-总进价)。
(1)设商场购进碳酸饮料y箱,直接写出y与x的函数解析式;
(2)求总利润w关于x的函数解析式;
(3)如果购进两种饮料的总费用不超过2100元,那么该商场如何进货才能获利最多?并求出最大利润。
饮料
果汁饮料
碳酸饮料
进价(元/箱)
40
25
售价(元/箱)
52
32
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
相关试题

