搜索
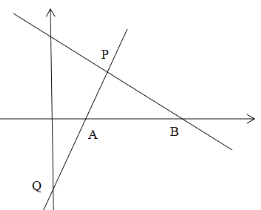
【题目】在平面直角坐标系中，直线y1=kx+b经过点P（2，2）和点Q（0，﹣2），与x轴交于点A，与直线y2=mx+n交于点P．
（1）求出直线y1=kx+b的解析式；
（2）当m＜0时，直接写出y1＜y2时自变量x的取值范围；
（3）直线y2=mx+n绕着点P任意旋转，与x轴交于点B，当△PAB是等腰三角形时，点B有几种位置？请你分别求出点B的坐标．
参考答案：
【答案】（1）y1=2x－2（2）x＜2（3）（
+1，0）、（3，0）、（3.5，0）、（1－，0）
【解析】
（1）运用待定系数法求解即可；
（2）根据m＜0时，由函数图象即可确定当y1＜y2时自变量x的取值范围；
（3）分m＞0时和m＜0时两种情况进行讨论，根据等腰三角形的性质确定点B的位置即可.
（1）把P（2，2）和点Q（0，﹣2）代入y1=kx+b得，
，解得
，
所以，直线的解析式为：y1=2x－2
（2）当m＜0时，由图象得，y1＜y2时自变量x的取值范围x＜2；
（3）过点P作PM⊥x轴，交于点M
由题意可知A（1，0），M（2，0），AP=，AM=1
当m＞0时，点B有3种位置使得△PAB为等腰三角形
①当AP=AB时，AB=，∴B（+1，0）
②当PA=PB时，AB=2AM=2，∴B（3，0）
③当BA=BP时，设AB=x，由等面积法可得S△ABP=2x=
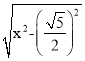
解得x=2.5，∴B（3.5，0）
当m＜0时，点B有1种位置使得△PAB为等腰三角形
当AB=AP时，OB=－1，∴B（1－，0）
综上所述，点B有4种位置使得△PAB为等腰三角形，坐标分别为（+1，0）、（3，0）、（3.5，0）、（1－，0）
-
科目： 来源： 题型：
查看答案和解析>>【题目】数轴是学习有理数的一种重要工具，任何有理数都可以用数轴上的点表示，这样能够运用数形结合的方法解决一些问题.
如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”.图中点A表示－10，点B表示10，点C表示18，我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发，以2单位秒的速度沿着折线数抽”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点Q从点C出发，以1单位秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速.当点P到达点C时，两点都停上远动.设运动的时间为1秒.问：
(1)t＝2秒时，点P在“折线数轴”上所对应的数是_______；点P到点Q的距离是_____单位长度；
(2)动点P从点4运动至C点需要_______秒；
(3)P、Q两点相遇时，求出t的值和此时相遇点M在“折线数轴”上所对应的数；
(4)如果动点P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等，直接写出t的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A（4，0）及在第一象限的动点P（x，y），且x+y=5，0为坐标原点，设△OPA的面积为S．
（1）求S关于x的函数表达式；
（2）求x的取值范围；
（3）当S=4时，求P点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD边长为3，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB延长线于点F，则EF的长为__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】平面直角坐标系xOy中，点A（x1，y1）与B（x2，y2），如果满足x1+x2=0，y1﹣y2=0，其中x1≠x2，则称点A与点B互为反等点．已知：点C（3，4）
（1）下列各点中， 与点C互为反等点；
D（﹣3，﹣4），E（3，4），F（﹣3，4）
（2）已知点G（﹣5，4），连接线段CG，若在线段CG上存在两点P，Q互为反等点，求点P的横坐标xP的取值范围；
（3）已知⊙O的半径为r，若⊙O与（2）中线段CG的两个交点互为反等点，求r的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于
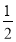MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（ ）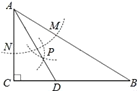
①AD是∠BAC的平分线；②∠ADC=60°； ③点D在AB的中垂线上；④S△DAC：S△ABC=1：3．
A. 1B. 2C. 3D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：关于x、y的方程组
的解为非负数．（1）求a的取值范围；
（2）化简|2a+4|﹣|a﹣1|；
（3）在a的取值范围内，a为何整数时，使得2ax+3x＜2a+3解集为x＞1．
相关试题
