【题目】数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.
如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,以2单位秒的速度沿着折线数抽”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.当点P到达点C时,两点都停上远动.设运动的时间为1秒.问:
(1)t=2秒时,点P在“折线数轴”上所对应的数是_______;点P到点Q的距离是_____单位长度;
(2)动点P从点4运动至C点需要_______秒;
(3)P、Q两点相遇时,求出t的值和此时相遇点M在“折线数轴”上所对应的数;
(4)如果动点P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等,直接写出t的值.

参考答案:
【答案】(1)![]() (2)10 (3)
(2)10 (3)![]() ,
,![]() (4)2,6.5,11,17
(4)2,6.5,11,17
【解析】
(1)根据题意计算出![]() 秒时所运动的长度即可,进而算出P、Q之间的距离;
秒时所运动的长度即可,进而算出P、Q之间的距离;
(2)从点4到C点需要经过OB上一段距离以及BC的长,把它们所需时间相加即可;
(3)根据相遇的时候两点所运动的路程=28,可以列出方程,解出t的值即可;
(4)根据不同的情况进行讨论即可,分为4种情况解出t值.
解:
(1)当![]() 秒时,点P运动了4,此时对应的数为:
秒时,点P运动了4,此时对应的数为:![]() ,
,
点Q运动了2,此时Q对应的数为:![]() ,
,
(2)![]() 点P到点Q的距离是
点P到点Q的距离是![]() 单位长度.
单位长度.
此时分为三段:PO、OB、BC,
点P在点4运动到B点需要时间:![]() (秒),
(秒),
从B到C需要时间:![]() (秒),
(秒),
![]() 一共需要:
一共需要:![]() (秒);
(秒);
(3)经分析可得相遇一定在OB上,设经过时间t两者相遇,
此时在OB上点Q的时间为:![]() ,
,
在OB上点P的时间为:![]() ,
,
根据总路程为28,列出方程:
![]()
解得:![]() ,
,
即:经过![]() 秒,P、Q两点相遇,
秒,P、Q两点相遇,
此时对应的数为:![]() .
.
(4)动点P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等,有4种可能:
①动点Q在CB上,动点P在AO上,
则:![]() ,解得:
,解得:![]() .
.
②动点Q在CB上,动点P在OB上,
则:![]() ,解得:
,解得:![]() .
.
③动点Q在BO上,动点P在OB上,
则:![]() ,解得:
,解得:![]() .
.
④动点Q在OA上,动点P在BC上,
则:![]() ,解得:
,解得:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段 AB=12cm,点 C 为 AB 上的一个动点,点 D,E 分别是 AC 和 BC的中点.
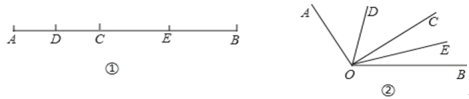
(1)若 AC=4cm,求 DE 的长.
(2)若 AC=acm(不超过 12cm),求 DE 的长.
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点 C 画射线OC,若OD,OE 分别平分∠AOC 和∠BOC,求∠DOE 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习兴趣小组参加一次单元测验,成绩统计情况如下表.
分 数
73
74
75
76
77
78
79
82
83
84
86
88
90
92
人 数
1
1
5
4
3
2
3
1
1
1
2
3
1
2
(1)该兴趣小组有多少人?
(2)兴趣小组本次单元测试成绩的平均数、中位数、众数各是多少?
(3)老师打算为兴趣小组下单元考试设定一个新目标,学生达到或超过目标给予奖励,并希望小组 三分之一左右的优秀学生得到奖励,请你帮老师从平均数、中位数、众数三个数中选择一个比较恰 当的目标数;如果计划让一半左右的人都得到奖励,确定哪个数作为目标恰当些?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在
 处,规定向北方向为正,当天行驶纪录如下(单位:千米)
处,规定向北方向为正,当天行驶纪录如下(单位:千米) ,
, ,
, ,
,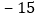 ,
, ,
, ,
, ,
,
 在岗亭何方?距岗亭多远?
在岗亭何方?距岗亭多远? 在行驶过程中,最远处离出发点有多远?
在行驶过程中,最远处离出发点有多远? 若摩托车行驶
若摩托车行驶 千米耗油
千米耗油 升,这一天共耗油多少升?
升,这一天共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(4,0)及在第一象限的动点P(x,y),且x+y=5,0为坐标原点,设△OPA的面积为S.
(1)求S关于x的函数表达式;
(2)求x的取值范围;
(3)当S=4时,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

-
科目: 来源: 题型:
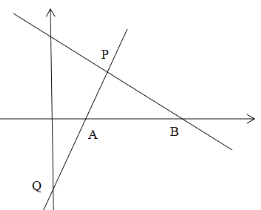
查看答案和解析>>【题目】在平面直角坐标系中,直线y1=kx+b经过点P(2,2)和点Q(0,﹣2),与x轴交于点A,与直线y2=mx+n交于点P.
(1)求出直线y1=kx+b的解析式;
(2)当m<0时,直接写出y1<y2时自变量x的取值范围;
(3)直线y2=mx+n绕着点P任意旋转,与x轴交于点B,当△PAB是等腰三角形时,点B有几种位置?请你分别求出点B的坐标.
相关试题

