【题目】平面直角坐标系xOy中,点A(x1,y1)与B(x2,y2),如果满足x1+x2=0,y1﹣y2=0,其中x1≠x2,则称点A与点B互为反等点.已知:点C(3,4)
(1)下列各点中, 与点C互为反等点;
D(﹣3,﹣4),E(3,4),F(﹣3,4)
(2)已知点G(﹣5,4),连接线段CG,若在线段CG上存在两点P,Q互为反等点,求点P的横坐标xP的取值范围;
(3)已知⊙O的半径为r,若⊙O与(2)中线段CG的两个交点互为反等点,求r的取值范围.
参考答案:
【答案】(1点F;(2) ﹣3≤xP≤3,且xp≠0;(3) 4<r≤5.
【解析】分析:(1)根据互为反等点的意义,得结论;
(2)因为点P、Q是线段CG上的互反等点,根据(1)的结论,可确定点P的横坐标xP的取值范围;
(3)根据圆与线段CG相离、相切、相交情况及互为反等点的定义,讨论得出圆的半径的取值范围.
详解:(1)因为3+(﹣3)=0,4﹣4=0
所以点(﹣3,4)与点(3,4)互为相反等点.
故答案为:点F.
(2)由于点C与点F互为反等点.
又因为点P,Q是线段CG上的反等点,
所以点P的横坐标xP的取值范围为:﹣3≤xP≤3,且xp≠0.
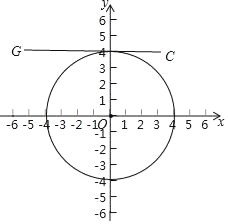
(3)如图所示,当
⊙O与CG相离时,此时⊙O与线段CG没有互为反等点;
当⊙O与CG相切时,此时r=4,⊙O与线段CG没有互为反等点;
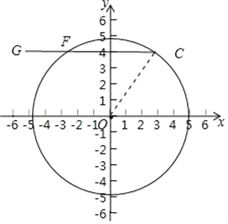
⊙O与CG相交于点C时,此时r=![]() =5.⊙O与线段CG有互为反等点;
=5.⊙O与线段CG有互为反等点;
当r>4,时,⊙O与线段CG有一个交点或者没有交点,
所以没有互为反等点.
综上当4<r≤5时,⊙O与线段CG有两个交点,这两个交点互为反等点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(4,0)及在第一象限的动点P(x,y),且x+y=5,0为坐标原点,设△OPA的面积为S.
(1)求S关于x的函数表达式;
(2)求x的取值范围;
(3)当S=4时,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

-
科目: 来源: 题型:
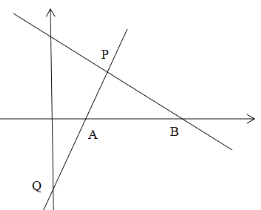
查看答案和解析>>【题目】在平面直角坐标系中,直线y1=kx+b经过点P(2,2)和点Q(0,﹣2),与x轴交于点A,与直线y2=mx+n交于点P.
(1)求出直线y1=kx+b的解析式;
(2)当m<0时,直接写出y1<y2时自变量x的取值范围;
(3)直线y2=mx+n绕着点P任意旋转,与x轴交于点B,当△PAB是等腰三角形时,点B有几种位置?请你分别求出点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )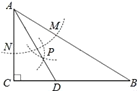
①AD是∠BAC的平分线;②∠ADC=60°; ③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x、y的方程组
 的解为非负数.
的解为非负数.(1)求a的取值范围;
(2)化简|2a+4|﹣|a﹣1|;
(3)在a的取值范围内,a为何整数时,使得2ax+3x<2a+3解集为x>1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B 两乡分别由大米 200 吨、300 吨.现将这些大米运至 C、D 两个粮站储存.已知 C 粮站可 储存 240 吨,D 粮站可储存 200 吨,从 A 乡运往 C、D 两处的费用分别为每吨 20 元和 25 元,B 乡 运往 C、D 两处的费用分别为每吨 15 元和 18 元.设 A 乡运往 C 粮站大米 x 吨.A、B 两乡运往两 个粮站的运费分别为 yA、yB 元.
(1)请填写下表,并求出 yA、yB 与 x 的关系式:
C 站
D 站
总计
A 乡
x 吨
200 吨
B 乡
300 吨
总计
240 吨
260 吨
500 吨
(2)试讨论 A、B 乡中,哪一个的运费较少;
(3)若 B 乡比较困难,最多只能承受 4830 元费用,这种情况下,运输方案如何确定才能使总运费 最少?最少的费用是多少?
相关试题

