【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论: ①AE=CF;
②△EPF是等腰直角三角形;
③S四边形AEPF= ![]() S△ABC;
S△ABC;
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合) BE+CF=EF.
上述结论中始终正确的有( )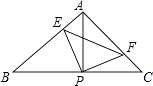
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:∵∠APE、∠CPF都是∠APF的余角, ∴∠APE=∠CPF,
∵AB=AC,∠BAC=90°,P是BC中点,
∴AP=CP,
又∵AP=CP,∠EPA=∠FPC,∠EAP=∠FCP=45°
∴△APE≌△CPF(ASA),同理可证△APF≌△BPE,
∴AE=CF,△EPF是等腰直角三角形,S四边形AEPF= ![]() S△ABC , ①②③正确;
S△ABC , ①②③正确;
故AE=FC,BE=AF,
∴AF+AE>EF,
∴BE+CF>EF,故④不成立.
始终正确的是①②③.故选C.
【考点精析】通过灵活运用等腰直角三角形和旋转的性质,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.
-
科目: 来源: 题型:
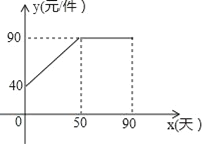
查看答案和解析>>【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天)
1
30
60
90
每天销售量p(件)
198
140
80
20
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有若干个数,第一个数记为a1 , 第二个数记为a2 , …第n个数记为an , 若a1=2,从第二个数起,每个数都等于“1与前面那个数的差的倒数”,
(1)计算:a3=
(2)a2015= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,求方程的另一个根x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)16﹣23+24﹣17
(2)﹣23÷(﹣ )÷(﹣
)÷(﹣  )2
)2
(3)( ﹣
﹣  ﹣
﹣  )×(﹣18)
)×(﹣18)
(4)(﹣1)10﹣(﹣3)×| ﹣
﹣  |÷
|÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子中去括号错误的是( )
A.5x﹣(x﹣2y)=5x﹣x+2y
B.2a2+(3a﹣b)=2a2+3a﹣b
C.(x﹣2y)﹣(x2﹣y2)=x﹣2y﹣x2+y2
D.3x2﹣3(x+6)=3x2﹣3x﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b是一元二次方程x2-x-2=0的两根,求a+b的值
相关试题

