Question

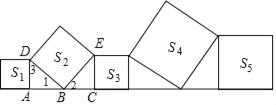
【题目】如图，五个正方形面积分别记为S1，S2，S3，S4，S5，若S1＝2，S3＝3，S5＝5，则S2+S4＝_____．

Answer 1

【答案】13．

【解析】

根据全等三角形的判定定理得到△ABD≌△CEB，根据全等三角形的性质得到AD＝BC，AB＝CE，根据勾股定理得到BD2＝AD2+AB2＝AD2+CE2，于是易得结论．

解：如图，∵∠DAB＝∠BCE＝∠DBE＝90°，

∴∠1+∠3＝∠1+∠2＝90°，

∴∠3＝∠2，

在△ABD与△CEB中，

，

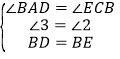∴△ABD≌△CEB（AAS），

∴AD＝BC，AB＝CE，

∵BD2＝AD2+AB2＝AD2+CE2，

∴S2＝S1+S3＝5，

同理，S4＝S3+S5＝8，

∴S2+S4＝13，

故答案为：13．