【题目】一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函数关系，其部分图象如图所示．

（1）求y关于x的函数关系式；（不需要写定义域）

（2）已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？

参考答案：

【答案】（1）该一次函数解析式为y=﹣x+60．（2）在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是10千米．

【解析】

（1）根据函数图象中点的坐标利用待定系数法求出一次函数解析式；

（2）根据一次函数图象上点的坐标特征即可求出剩余油量为8升时行驶的路程，即可求得答案.

（1）设该一次函数解析式为y=kx+b，

将（150，45）、（0，60）代入y=kx+b中，得

，解得：，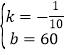

∴该一次函数解析式为y=﹣x+60；

（2）当y=﹣x+60=8时，

解得x=520，

即行驶520千米时，油箱中的剩余油量为8升．

530﹣520=10千米，

油箱中的剩余油量为8升时，距离加油站10千米，

∴在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是10千米．

关闭