搜索
【题目】计算：（ 
）﹣2﹣|﹣7|+（5 
﹣ 
+25）0﹣（﹣1）2014 ．
参考答案：
【答案】解：原式=9﹣7+1﹣1=2．
【解析】原式第一项利用负指数幂法则计算，第二项利用绝对值的代数意义化简，第三项利用零指数幂法则计算，最后一项利用乘方的意义计算即可得到结果．
【考点精析】根据题目的已知条件，利用零指数幂法则和整数指数幂的运算性质的相关知识可以得到问题的答案，需要掌握零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，AB∥CD，∠A = ∠D，试说明 AC∥DE 成立的理由.
下面是彬彬同学进行的推理，请你将彬彬同学的推理过程补充完整。
解：∵ AB ∥ CD （已知）
∴ ∠A = （两直线平行，内错角相等）
又∵ ∠A = ∠D（ ）
∴ ∠ = ∠ （等量代换）
∴ AC ∥ DE （ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=1，将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′，则图中阴影部分的面积是 ．
-
科目： 来源： 题型：
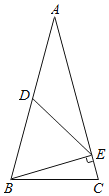
查看答案和解析>>【题目】如图，已知：在△ABC中，∠C=∠ABC，BE⊥AC，△BDE是正三角形．求∠C的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(10分)已知△ABC是等边三角形，点D是直线BC上一点，以AD为一边在AD的右侧作等边△ADE.
(1)如图①，点D在线段BC上移动时，直接写出∠BAD和∠CAE的大小关系；
(2)如图②，点D在线段BC的延长线上移动时，猜想∠DCE的大小是否发生变化．若不变请求出其大小；若变化，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，任意两点A (x1,y1)，B (x2,y2)规定运算：①A
B=( x1+ x2, y1+ y2)；②A
B= x1 x2+y1 y2③当x1= x2且y1= y2时A=B有下列四个命题：（1）若A(1，2)，B(2，–1)，则A
B=(3,1)，AB=0；（2）若A
B=BC，则A=C；（3）若AB=BC，则A=C；（4）对任意点A、B、C，均有（A
B ) C=A ( BC )成立.其中正确命题的个数为（ ）A. 1个 B. 2个 C. 3个 D.4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB‖CD,∠EAF =
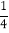∠EAB,∠ECF=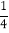∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
相关试题
