Question

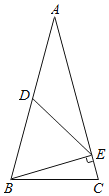
【题目】如图，已知：在△ABC中，∠C=∠ABC，BE⊥AC，△BDE是正三角形．求∠C的度数．

Answer 1

【答案】75°．

【解析】本题首先由等边三角形的性质及垂直定义得到∠DBE=60°，∠BEC=90°，再根据等腰三角形的性质可以得出∠EBC=∠ABC-60°=∠C-60°，最后根据三角形内角和定理得出关系式∠C-60°+∠C=90°解出即可．

解：∵△BDE是正三角形，

∴∠DBE=60°；

∵在△ABC中，∠C=∠ABC，BE⊥AC，

∴∠C=∠ABC=∠ABE+∠EBC则∠EBC=∠ABC﹣60°=∠C﹣60°，∠BEC=90°；

∴∠EBC+∠C=90°，即∠C﹣60°+∠C=90°

解得∠C=75°．

“点睛”本题主要考查等腰三角形的性质及等边三角形的性质及垂直定义，解题的关键是根据三角形内角和定理列出符合题意的简易方程，从而求出结果．