【题目】二次函数![]() 图象如图,下列结论:
图象如图,下列结论:
①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④
;④![]() .
.
其中正确的有________.

参考答案:
【答案】②③
【解析】
由抛物线开口方向得到a<0,由抛物线的对称轴为直线![]()
得到b>0,由抛物线与y轴的交点在x轴上方得到c>0,则abc<0;由于抛物线的对称轴为直线![]() 则b=-2a,得到2a+b=0;由于x=-1时,y<0,于是有a-b+c<0.
则b=-2a,得到2a+b=0;由于x=-1时,y<0,于是有a-b+c<0.
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=b2a>0,
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线的对称轴为直线![]()
∴b=2a>0,
∴2a+b=0,所以②正确;
∵抛物线的对称轴为x=1,
∴当x=1时的函数值是最大值,
∴![]() (x≠1),
(x≠1),
∴![]() 所以③正确;
所以③正确;
∵x=1时,y<0,
∴ab+c<0,所以④错误.
故答案为:②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在
,在 中,
中, 、
、 的平分线相交于点O
的平分线相交于点O 若
若 ,求
,求 的度数;
的度数; 若
若 ,则
,则 ______ ;
______ ; 若
若 ,则
,则 ______ ;
______ ; 如图
如图 ,在
,在 中的外角平分线相交于点
中的外角平分线相交于点 ,
, ,求
,求 的度数;
的度数; 上面
上面 ,
, 两题中的
两题中的 与
与 有怎样的数量关系?
有怎样的数量关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①AP⊥BC;②AS=AR;③QP∥AR;④△BRP≌△QSP.正确的有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).

(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的△A′B′C′,并写出点B′的坐标;
(3)P是x轴上的动点,在图中找出使△A′BP周长最短时的点P,直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 ,它的图象经过点
,它的图象经过点 .
.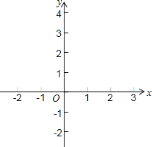
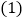 若该图象与
若该图象与 轴的一个交点为
轴的一个交点为 .
.①求二次函数
 的表达式;
的表达式;②出该二次函数的大致图象,并借助函数图象,求不等式
 的解集;
的解集; 当
当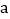 取
取 ,
, 时,二次函数图象与
时,二次函数图象与 轴正半轴分别交于点
轴正半轴分别交于点 ,点
,点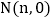 .如果点
.如果点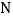 在点
在点 的右边,且点
的右边,且点 和点
和点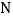 都在点
都在点 的右边.试比较
的右边.试比较 和
和 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂设门市部专卖某产品,该产品每件成本
 元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:每件销售价(元)
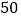


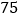
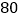
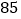
…
每天售出件数
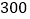
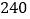
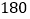
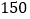
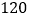
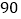
…
假设当天定的售价是不变的,且每天销售情况均服从这种规律.
 观察这些统计数据,找出每天售出件数
观察这些统计数据,找出每天售出件数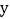 与每件售价
与每件售价 (元)之间的函数关系,并写出该函数关系式.
(元)之间的函数关系,并写出该函数关系式.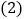 门市部原设有两名营业员,但当销售量较大时,在每天售出量超过
门市部原设有两名营业员,但当销售量较大时,在每天售出量超过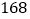 件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为
件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为 元.求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)
元.求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,二次函数
中,二次函数 的图象与
的图象与 轴正半轴交于
轴正半轴交于 点.
点.
 求证:该二次函数的图象与
求证:该二次函数的图象与 轴必有两个交点;
轴必有两个交点; 设该二次函数的图象与
设该二次函数的图象与 轴的两个交点中右侧的交点为点
轴的两个交点中右侧的交点为点 ,若
,若 ,将直线
,将直线 向下平移
向下平移 个单位得到直线
个单位得到直线 ,求直线
,求直线 的解析式;
的解析式; 在
在 的条件下,设
的条件下,设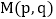 为二次函数图象上的一个动点,当
为二次函数图象上的一个动点,当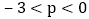 时,点
时,点 关于
关于 轴的对称点都在直线
轴的对称点都在直线 的下方,求
的下方,求 的取值范围.
的取值范围.
相关试题

