【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①AP⊥BC;②AS=AR;③QP∥AR;④△BRP≌△QSP.正确的有( )

A.1个B.2个C.3个D.4个
参考答案:
【答案】D
【解析】
根据到角的两边的距离相等的点在角的平分线上可得AP平分∠BAC,根据等腰三角形“三线合一”的性质判断出①正确;根据HL证明Rt△APR≌Rt△APS,即可判断②正确;根据等边对等角的性质可得∠APQ=∠PAQ,根据三角形外角的性质得到然后得到∠PQC=2∠PAC=60°=∠BAC,然后根据同位角相等两直线平行可得QP∥AB,从而判断出③正确,④由③易证△QPC是等边三角形,得到PQ=PC,等量代换得到BP=PQ,用HL证明Rt△BRP≌Rt△QSP,即可得到④正确.
∵△ABC是等边三角形,PR⊥AB,PS⊥AC,且PR=PS,∴P在∠A的平分线上.
∵AB=AC,∴AP⊥BC,故①正确;
∵PA=PA,PR=PS,∴Rt△APR≌Rt△APS,∴AS=AR,故②正确;
∵AQ=PQ,∴∠APQ=∠PAQ,∴∠PQC=2∠PAC=60°=∠BAC,∴PQ∥AR,故③正确;
由③得:△PQC是等边三角形,∴△PQS≌△PCS,∴PQ=PC.
又∵AB=AC,AP⊥BC,∴BP=PC,∴BP=PQ.
∵PR=PS,∴Rt△BRP≌Rt△QSP,故④也正确.
∵①②③④都正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数
 ,有下列说法:
,有下列说法:①它的图象与
 轴有两个公共点;
轴有两个公共点;②如果当
 时
时 随
随 的增大而减小,则
的增大而减小,则 ;
;③如果将它的图象向左平移
 个单位后过原点,则
个单位后过原点,则 ;
;④如果当
 时的函数值与
时的函数值与 时的函数值相等,则当
时的函数值相等,则当 时的函数值为
时的函数值为 .
.其中正确的说法是________.(把你认为正确说法的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+2分别与x轴、y轴相交于点A、点B
x+2分别与x轴、y轴相交于点A、点B
(1)求点A和点B的坐标;
(2)若点P是y轴上的一点,设△AOB、△ABP的面积分别为S△AOB与S△ABP,且S△ABP=2S△AOB,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在
,在 中,
中, 、
、 的平分线相交于点O
的平分线相交于点O 若
若 ,求
,求 的度数;
的度数; 若
若 ,则
,则 ______ ;
______ ; 若
若 ,则
,则 ______ ;
______ ; 如图
如图 ,在
,在 中的外角平分线相交于点
中的外角平分线相交于点 ,
, ,求
,求 的度数;
的度数; 上面
上面 ,
, 两题中的
两题中的 与
与 有怎样的数量关系?
有怎样的数量关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).

(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的△A′B′C′,并写出点B′的坐标;
(3)P是x轴上的动点,在图中找出使△A′BP周长最短时的点P,直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 图象如图,下列结论:
图象如图,下列结论:①
 ;②
;② ;③当
;③当 时,
时, ;④
;④ .
.其中正确的有________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 ,它的图象经过点
,它的图象经过点 .
.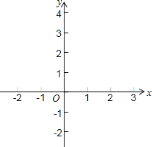
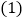 若该图象与
若该图象与 轴的一个交点为
轴的一个交点为 .
.①求二次函数
 的表达式;
的表达式;②出该二次函数的大致图象,并借助函数图象,求不等式
 的解集;
的解集; 当
当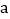 取
取 ,
, 时,二次函数图象与
时,二次函数图象与 轴正半轴分别交于点
轴正半轴分别交于点 ,点
,点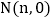 .如果点
.如果点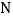 在点
在点 的右边,且点
的右边,且点 和点
和点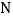 都在点
都在点 的右边.试比较
的右边.试比较 和
和 的大小.
的大小.
相关试题

