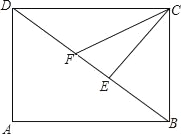
【题目】如图,矩形ABCD中,CE⊥BD于E,CF平分∠DCE与DB交于点F.
(1)求证:BF=BC;
(2)若AB=4cm,AD=3cm,求CF的长.
参考答案:
【答案】(1)见解析,(2)CF=![]() cm.
cm.
【解析】
(1)要求证:BF=BC只要证明∠CFB=∠FCB就可以,从而转化为证明∠BCE=∠BDC就可以;
(2)已知AB=4cm,AD=3cm,就是已知BC=BF=3cm,CD=4cm,在直角△BCD中,根据三角形的面积等于![]() BDCE=
BDCE=![]() BCDC,就可以求出CE的长.要求CF的长,可以在直角△CEF中用勾股定理求得.其中EF=BF-BE,BE在直角△BCE中根据勾股定理就可以求出,由此解决问题.
BCDC,就可以求出CE的长.要求CF的长,可以在直角△CEF中用勾股定理求得.其中EF=BF-BE,BE在直角△BCE中根据勾股定理就可以求出,由此解决问题.
证明:(1)∵四边形ABCD是矩形,∴∠BCD=90°,
∴∠CDB+∠DBC=90°.
∵CE⊥BD,∴∠DBC+∠ECB=90°.
∴∠ECB=∠CDB.
∵∠CFB=∠CDB+∠DCF,∠BCF=∠ECB+∠ECF,∠DCF=∠ECF,
∴∠CFB=∠BCF
∴BF=BC
(2)∵四边形ABCD是矩形,∴DC=AB=4(cm),BC=AD=3(cm).
在Rt△BCD中,由勾股定理得BD=![]() .
.
又∵BDCE=BCDC,
∴CE=![]() .
.
∴BE=![]() .
.
∴EF=BF﹣BE=3﹣![]() .
.
∴CF=![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(a,m)、B(2a,n)是反比例函数y=
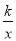 (k>0)与一次函数y=-
(k>0)与一次函数y=- x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.
x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.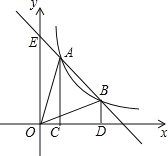
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
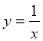 和一次函数y=-x+a-1(a为常数)
和一次函数y=-x+a-1(a为常数)(1)当a=5时,求反比例函数与一次函数的交点坐标(5分)
(2)是否存在实数a,使反比例函数与一次函数有且只有一个交点,如果存在,求出实数a,如果不存在,说明理由(5分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”期间,小明一家自驾游去了离家200km的某地,如图是他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象.根据图象,解答下列问题:
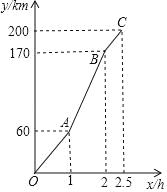
(1)点A的实际意义是 ;
(2)求出线段AB的函数表达式;
(3)他们出发2.3h时,距目的地还有多少km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,对于点P(x,y)和Q(﹣x,y′),给出如下定义:
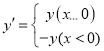 ,称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(﹣1,2),点(﹣1,2)的“可控变点”为点(1,﹣2)
,称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(﹣1,2),点(﹣1,2)的“可控变点”为点(1,﹣2)根据定义,解答下列问题;
(1)点(3,4)的“可控变点”为点 .
(2)点P1的“可控变点”为点P2,点P2的“可控变点”为点P3,点P3的“可控变点”为点P4,…,以此类推.若点P2018的坐标为(3,a),则点P1的坐标为 .
(3)若点N(a,3)是函数y=﹣x+4图象上点M的“可控变点”,求点M的坐标.
-
科目: 来源: 题型:
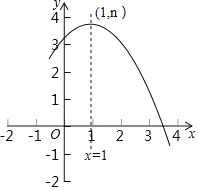
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其顶点坐标为(1,n),且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:
①ac

②a﹣b+c>0;
③当
 时,y随x的增大而增大
时,y随x的增大而增大若(﹣
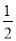 ,y1),(
,y1),( ,y2)是抛物线上的两点,则y1
,y2)是抛物线上的两点,则y1 y2;
y2;④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市有
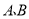 两种出租车.
两种出租车.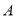 的计价方式为:当行驶路程不超过
的计价方式为:当行驶路程不超过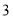 千米时收费
千米时收费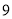 元,每超过
元,每超过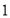 千米则另外收费
千米则另外收费 元(不足
元(不足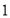 千米按
千米按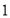 千米收费);
千米收费);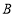 的计价方式为:当行驶路程不超过
的计价方式为:当行驶路程不超过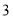 千米时收费
千米时收费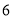 元,每超过
元,每超过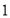 千米则另外收费
千米则另外收费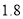 元(不足
元(不足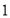 千米按
千米按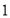 千米收费).某人到该市出差,需要乘坐的路程为
千米收费).某人到该市出差,需要乘坐的路程为 千米.
千米. (1)当
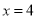 时,请分别求出乘坐
时,请分别求出乘坐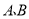 两种出租车的费用;
两种出租车的费用; (2)①此人若乘坐
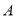 种出租车比乘坐
种出租车比乘坐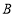 种出租车的费用省
种出租车的费用省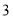 元,则求
元,则求 的值;
的值; ②某人乘坐的路程大于
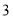 千米,请帮他规划如何选择乘坐哪种出租车较合算?
千米,请帮他规划如何选择乘坐哪种出租车较合算?
相关试题

