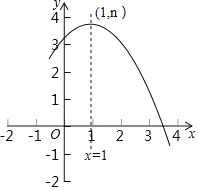
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其顶点坐标为(1,n),且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:
①ac![]()
②a﹣b+c>0;
③当![]() 时,y随x的增大而增大
时,y随x的增大而增大
若(﹣![]() ,y1),(
,y1),(![]() ,y2)是抛物线上的两点,则y1
,y2)是抛物线上的两点,则y1![]() y2;
y2;
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】试题解析::∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点在(3,0)和(4,0)之间,
∴抛物线与x轴的一个交点在(-2,0)和(-1,0)之间,
∴x=-1时,y>0,
即a-b+c>0,所以①正确;
∵抛物线的对称轴为x=-![]() =1,
=1,
∴b=-2a,
∴3a+b=3a-2a=a≠0,所以②错误;
∵点(-![]() ,y1)到直线x=1的距离比点(
,y1)到直线x=1的距离比点(![]() ,y2)到直线x=1的距离大,
,y2)到直线x=1的距离大,
而抛物线开口向下,
∴y1<y2,所以③正确;
∵x=1时,y有最大值为n,
∴抛物线与直线y=n-1有两个交点,
∴一元二次方程ax2+bx+c=n-1有两个不相等的实数根,所以④正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”期间,小明一家自驾游去了离家200km的某地,如图是他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象.根据图象,解答下列问题:
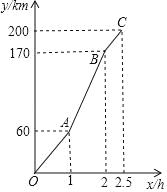
(1)点A的实际意义是 ;
(2)求出线段AB的函数表达式;
(3)他们出发2.3h时,距目的地还有多少km?
-
科目: 来源: 题型:
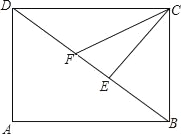
查看答案和解析>>【题目】如图,矩形ABCD中,CE⊥BD于E,CF平分∠DCE与DB交于点F.
(1)求证:BF=BC;
(2)若AB=4cm,AD=3cm,求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,对于点P(x,y)和Q(﹣x,y′),给出如下定义:
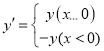 ,称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(﹣1,2),点(﹣1,2)的“可控变点”为点(1,﹣2)
,称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(﹣1,2),点(﹣1,2)的“可控变点”为点(1,﹣2)根据定义,解答下列问题;
(1)点(3,4)的“可控变点”为点 .
(2)点P1的“可控变点”为点P2,点P2的“可控变点”为点P3,点P3的“可控变点”为点P4,…,以此类推.若点P2018的坐标为(3,a),则点P1的坐标为 .
(3)若点N(a,3)是函数y=﹣x+4图象上点M的“可控变点”,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市有
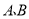 两种出租车.
两种出租车.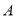 的计价方式为:当行驶路程不超过
的计价方式为:当行驶路程不超过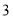 千米时收费
千米时收费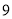 元,每超过
元,每超过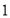 千米则另外收费
千米则另外收费 元(不足
元(不足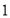 千米按
千米按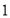 千米收费);
千米收费); 的计价方式为:当行驶路程不超过
的计价方式为:当行驶路程不超过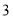 千米时收费
千米时收费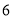 元,每超过
元,每超过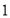 千米则另外收费
千米则另外收费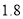 元(不足
元(不足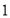 千米按
千米按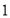 千米收费).某人到该市出差,需要乘坐的路程为
千米收费).某人到该市出差,需要乘坐的路程为 千米.
千米. (1)当
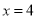 时,请分别求出乘坐
时,请分别求出乘坐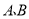 两种出租车的费用;
两种出租车的费用; (2)①此人若乘坐
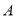 种出租车比乘坐
种出租车比乘坐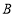 种出租车的费用省
种出租车的费用省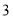 元,则求
元,则求 的值;
的值; ②某人乘坐的路程大于
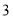 千米,请帮他规划如何选择乘坐哪种出租车较合算?
千米,请帮他规划如何选择乘坐哪种出租车较合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C17.
(1)写出点
 的坐标________
的坐标________(2)若P(50,m)在第17段抛物线C17上,则m=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点
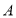 表示的数为
表示的数为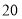 ,点
,点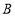 表示的数为
表示的数为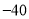 ,动点
,动点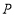 从点
从点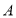 出发以每秒
出发以每秒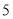 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点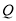 从原点出发以每秒
从原点出发以每秒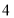 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点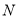 从点
从点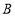 出发以每秒
出发以每秒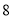 个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为
个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为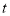 (秒).
(秒). 
(1)点
 在数轴上所表示的数分别为:____________,____________;
在数轴上所表示的数分别为:____________,____________;(2)当
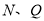 两点重合时,求此时点
两点重合时,求此时点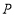 在数轴上所表示的数;
在数轴上所表示的数;
相关试题

