【题目】已知数轴上两点![]() 、
、![]() 对应的数分别为-1、3,点
对应的数分别为-1、3,点![]() 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为![]() .
.
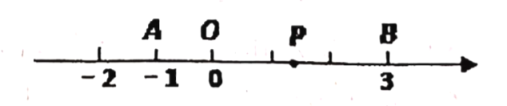
(1)若点![]() 到点
到点![]() 、点
、点![]() 的距离相等,则点
的距离相等,则点![]() 对应的数为 ;
对应的数为 ;
(2)利用数轴探究:找出满足![]() 的
的![]() 的所有值是 ;
的所有值是 ;
(3)当点![]() 以每秒6个单位长的速度从0点向右运动时,点
以每秒6个单位长的速度从0点向右运动时,点![]() 以每秒6个单位长的速度向右运动,点
以每秒6个单位长的速度向右运动,点![]() 以每秒钟5个单位长的速度向右运动,问它们同时出发,几秒后
以每秒钟5个单位长的速度向右运动,问它们同时出发,几秒后![]() 点到点
点到点![]() 、点
、点![]() 的距离相等?
的距离相等?
参考答案:
【答案】(1)1(2)-2或4(3)2秒或4秒
【解析】
(1)由点P到点A、点B的距离相等得点P是线段AB的中点,可确定点P对应的数;
(2)![]() 和
和![]() 分别表示P点到数轴上表示3和-1的点的距离,所以
分别表示P点到数轴上表示3和-1的点的距离,所以![]() 表示P点到数轴表示3和-1的点的距离之和为6,即表示P点到A、B两点的距离之和为6,分P点在A点左侧和P点在B点右侧讨论计算.
表示P点到数轴表示3和-1的点的距离之和为6,即表示P点到A、B两点的距离之和为6,分P点在A点左侧和P点在B点右侧讨论计算.
解:(1)∵点![]() 到点
到点![]() 、点
、点![]() 的距离相等,
的距离相等,
∴P点只能在A、B之间,
∴PA=PB=![]() AB=
AB=![]() ×4=2
×4=2
∴P点对应的数为1.
(2)![]() 表示P点到数轴表示3和-1的点的距离之和为6,即表示P点到A、B两点的距离之和为6
表示P点到数轴表示3和-1的点的距离之和为6,即表示P点到A、B两点的距离之和为6
①当P在A点左侧时,PA+PB=6,即PA+PA+4=6,
∴PA=1,∴x==-2;
②当P在B点右侧时,PA+PB=6,即PB+4+PB=6,
∴PB=1,∴x=4
③当P点A、B之间时,x不存在.
∴x的值为-2或4.
(3)设t秒后![]() 点到点
点到点![]() 、点
、点![]() 的距离相等,
的距离相等,
当P点在B左侧时 5t+3-6t=1, ∴t=2
当P点在B右侧时6t-(5t+3)=1,∴t=4
所以它们出发2秒或4秒后P到A、B点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是弧BC的中点,过点D作DE⊥AC,交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求AE的长.

-
科目: 来源: 题型:
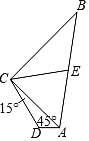
查看答案和解析>>【题目】已知四边形ABCD中,AB=10,BC=8,CD=
 ∠DAC=45°,∠DCA=15°.
∠DAC=45°,∠DCA=15°.(1)求△ADC的面积;
(2)若E为AB的中点,求线段CE的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知一次函数的图像直线AB经过点(0,6)和点(-2,0).
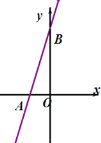
(1)求这个函数的解析式;
(2)直线AB与x轴交于点A,与y轴交于点B,求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数 a,b 在数轴上的位置如图所示,则下列各式中一定成立的是( )
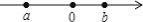
A. ﹣a>b B. a+b>0 C. a﹣b>a+b D. |a|+|b|<|a+b|
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合).
(1)如图1,当点D在线段BC上时,线段CE、BD之间的位置关系是__________,数量关系是___________;
(2)如图2,当点D在线段BC的延长线上时,探索AD、BD、CD三条线段之间的数量关系,写出结论并证明;
(3)若BD=
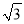 CD,直接写出∠BAD的度数。
CD,直接写出∠BAD的度数。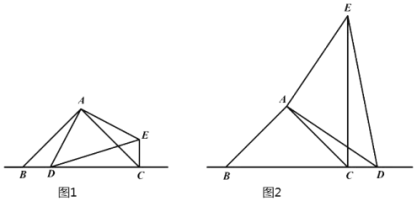
-
科目: 来源: 题型:
查看答案和解析>>【题目】哈市某专卖店销售某品牌服装,设服装进价为80元,当每件服装售价为240元时,月销售为200件,该专卖店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当每件价格每下降10元时,月销售量就会增加20件,设每件服装售价为x(元),该专卖店的月利润为y(元).
(1)求出y与x的函数关系式(不要求写出x的取值范围);
(2)该专卖店要获得最大月利润,售价应定为每件多少元?最大利润是多少?
相关试题

