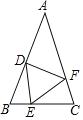
【题目】如图,在△ABC中AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)猜想:当∠A为多少度时,∠DEF=60°?请说明理由。
参考答案:
【答案】见解析
【解析】(1)通过全等三角形的判定定理SAS证得△DBE≌△RCF,由“全等三角形的对应边相等”推知DE=EF,所以△DEF是等腰三角形;
(2)由等腰△ABC的性质求得∠B=∠C=![]() (180°-40°)=70°,所以根据三角形内角和定理推知∠BDE+∠DEB=110°;再结合△DBE≌△ECF的对应角相等:∠BDE=∠FEC,故∠FEC+∠DEB=110°,易求∠DEF=70°;
(180°-40°)=70°,所以根据三角形内角和定理推知∠BDE+∠DEB=110°;再结合△DBE≌△ECF的对应角相等:∠BDE=∠FEC,故∠FEC+∠DEB=110°,易求∠DEF=70°;
(3)由(2)知,∠DEF=∠B,于是得到∠B=60°,推出△ABC是等边三角形,于是得到结论.
解:(1)因为AB=AC,所以∠B=∠C.
因为AD+EC=AB,AD+DB=AB,
所以BD=EC.
在△DBE和 △ECF中,因为BE=CF,∠B=∠C,BD=EC,
所以△DBE≌△ECF(SAS).
所以DE=EF.
所以△DEF是等腰三角形.
(2)因为∠A=40°,∠B=∠C,
所以∠B=∠C=70°.
因为△DBE≌△ECF,所以∠BDE=∠CEF.
因为∠DEC=∠DEF+∠FEC=∠B+∠BDE,
所以∠DEF=∠B.所以∠DEF=70°,
(3)当∠A为60°时,∠DEF=60°.理由如下:
由(2)知∠DEF=∠B.
若∠DEF=60°,则∠B=60°.
因为AB=AC,所以∠ABC是等边三角形.
所以∠A=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:4m2-n2=.
-
科目: 来源: 题型:
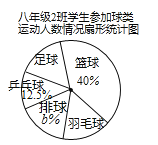
查看答案和解析>>【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)a= ,b= ;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
-
科目: 来源: 题型:
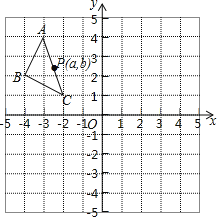
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1),且△A1B1C1与△ABC关于原点O成中心对称。
(1)画出△A1B1C1,并写出点A1的坐标;
(2)P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对应点为P'(a+3,b+1),请画出平移后的△A2B2C2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为奖励大学生创业,我市为在开发区创业的每位大学生提供无息贷款125000元,这个数据用科学记数法表示为(保留二位有效数字)( )
A.1.25×105
B.1.2×105
C.1.3×105
D.1.3×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两条边长分别是7和3,则此三角形的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4x2+mx+25是一个完全平方式,则m的值是 .
相关试题

