【题目】求一个正数的算术平方根,有些数可以直接求得,如![]() ,有些数则不能直接求得,如
,有些数则不能直接求得,如![]() ,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n | 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
(1)若![]() ,则
,则![]()
(2)根据你发现的规律,探究下列问题:已知![]() ≈1.435,则:
≈1.435,则:
①![]() ≈ ;
≈ ;
②![]() ≈ ;
≈ ;
(3)根据上述探究过程类比研究一个数的立方根已知![]() ≈1.260,则
≈1.260,则![]() ≈ .
≈ .
参考答案:
【答案】(1)10 ;(2)①0.1435 ② 143.5;(3)12.60 .
【解析】
(1)根据算术平方根的性质化简即可;
(2)从被开方数和算术平方根的小数点的移动位数考虑解答;
(3)根据(2)中的规律解答即可.
(1)![]() =10;
=10;
(2)观察表格可知:被开方数扩大或缩小102n倍,非负数的算术平方根就相应的扩大或缩小10n倍或者说成被开方数的小数点向左或向右移动2n位,算术平方根的小数点就向左或向右移动n位,∴![]() ;
;
(3)![]() ≈12.60.
≈12.60.
故答案为:(1)10;(2)被开方数的小数点向左或向右每移动2位,算术平方根的小数点就相应向左或向右移动1位,0.1435;143.5;(3)12.60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣8,0),点P的坐标为
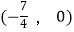 ,直线y=
,直线y=  x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.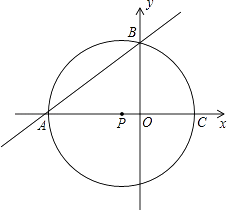
(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.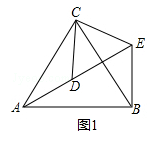
(1)证明:AD=BE;
(2)求∠AEB的度数.
(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.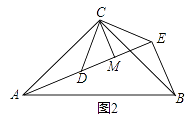
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元/件)
…
30
40
50
60
…
每天销售量y(件)
…
500
400
300
200
…
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;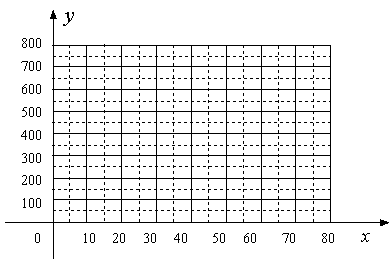
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.
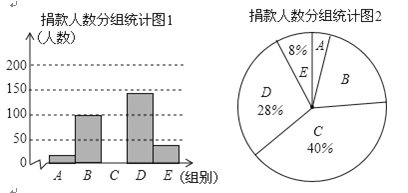
被调查的捐款人数分组统计表:
组别
捐款额x/元
人数
A
1≤x<10
a
B
10≤x<20
100
C
20≤x<30
______
D
30≤x<40
______
E
40≤x
______
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

相关试题

