【题目】某学校准备成立男女校足球队,为了解全校学生对足球的喜爱程度,该校设计了一个调查问卷,将喜爱程度分为A(非常喜欢)、B(喜欢)、C(不太喜欢),D(很不喜欢)四种类型,并派学生会会员进行市场调查,其中一名学生会会员小丽在校门口对上学学生进行了随机调查,并根据调查结果制成了如下两幅不完整的统计图,请结合统计图所给信息解答下列问题:
(1)在扇形统计图(图1)中C所占的百分比是 ;小丽本次抽样调查的人数共有 人;
请将折线统计图(图2)补充完整;
(2)为了解少数学生很不喜欢足球的原因,小丽决定在上述调查结果中从“很不喜欢”足球的学生里随机选
出两位进行回访,请你用列表法或画树状图的方法,求所选出的两位学生恰好是一男一女的概率.

参考答案:
【答案】(1)22%,50(2)![]()
【解析】
试题(1)用整体1减去A、B、D所占的百分比,剩下的就是图中C所占的百分比;用非常喜欢足球的人数除以所占的百分比,求出本次抽样调查的总人数,再分别求出不太喜欢足球的男生和很不喜欢足球的男生,从而补全统计图;
(2)先根据题意画出树状图,再根据概率公式即可求出答案.
试题解析:(1)在扇形统计图中C所占的百分比是:1﹣20%﹣52%﹣6%=22%;
小丽本次抽样调查的共有人数是:![]() =50(人);
=50(人);
不太喜欢足球的男生有:50×22%﹣5=6(人),
很不喜欢足球的男生有:50×6%﹣1=2(人),
补图如下:
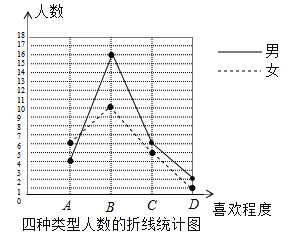
故答案为:22%,50;
(2)根据题意画图如下:
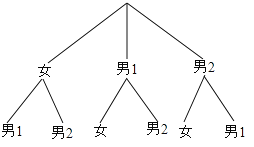
共有6中情况,选出的两位市民恰好都是男性的概率是![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣2,﹣1,0,1,2,3这六个数中,任取一个数作为a的值,恰好使得关于x、y的二元一次方程组
 有整数解,且方程ax2+ax+1=0有实数根的概率是_____.
有整数解,且方程ax2+ax+1=0有实数根的概率是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】从
 两水库向甲、乙两地调水,其中甲地需水
两水库向甲、乙两地调水,其中甲地需水 万吨,乙地需水
万吨,乙地需水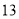 万吨,
万吨,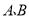 两水库各可调出水
两水库各可调出水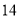 万吨,从
万吨,从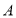 水库到甲地
水库到甲地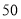 千米,到乙地
千米,到乙地 千米;从
千米;从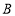 水库到甲地
水库到甲地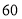 千米,到乙地
千米,到乙地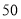 千米,设计一个调运方案使水的调运总量(单位:万吨千米)尽可能大。
千米,设计一个调运方案使水的调运总量(单位:万吨千米)尽可能大。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=
 (k≠0)的图象与一次函数y=ax+b(a≠0)的图象交于A、B两点,过点A作AH⊥y轴,垂足为H,若OH=4,sin∠AOH=
(k≠0)的图象与一次函数y=ax+b(a≠0)的图象交于A、B两点,过点A作AH⊥y轴,垂足为H,若OH=4,sin∠AOH= ,点B的坐标(6,n).
,点B的坐标(6,n).(1)求反比例函数和一次函数的解析式.
(2)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】创意产品蕴含着很多商机,我市某文化创意公司,销售A,B两种创意产品,其中A产品的定价是每件20元,B产品的定价是每件30元.
(1)该公司按定价售出A,B两种产品共600件,若销售总额不低于15000元,则至少销售B产品多少件?
(2)2017年8月,该公司按定价售出A产品300件,B产品400件.2017年9月,公司根据市场情况,适当调整A,B产品的售价,A产品的售价比定价增加了a%,销量与8月保持不变;B产品的售价比定价减少了a%,销量比8月份增加了a%,结果9月份A,B产品的销售总额比8月份增加了
 a%,求a的值.
a%,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一个三位正整数n各数位上的数字重新排列(含n本身)后,得到新的三位数
 (a<c),在所有重新排列大的数中,当|a+c﹣2b|最小时,我们称
(a<c),在所有重新排列大的数中,当|a+c﹣2b|最小时,我们称 是n的“天时数”,并规定F(n)=b2﹣ac.当|a+c﹣2b|最大时,我们称
是n的“天时数”,并规定F(n)=b2﹣ac.当|a+c﹣2b|最大时,我们称 是n的“地利数”,并规定G(n)=ac﹣b2.并规定M(n)=
是n的“地利数”,并规定G(n)=ac﹣b2.并规定M(n)= 是n的“人和数”,例如:215可以重新排列为125,152,215,因为|1+5﹣2×2|=2,|1+2﹣2×5|=7,|2+5﹣2×1|=5,且2<5<7,所以125是215的“天时数”F(125)=22﹣1×5=﹣1,152是215的“地利数”,G(152)=1×2﹣52=﹣23,M(215)=
是n的“人和数”,例如:215可以重新排列为125,152,215,因为|1+5﹣2×2|=2,|1+2﹣2×5|=7,|2+5﹣2×1|=5,且2<5<7,所以125是215的“天时数”F(125)=22﹣1×5=﹣1,152是215的“地利数”,G(152)=1×2﹣52=﹣23,M(215)=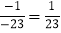 .
.(1)计算:F(168),G(168);
(2)设三位自然数s=100x+50+y(1≤x≤9,1≤y≤9,且x,y均为正整数),交换其个位上的数字与百位上的数字得到t,若s﹣t=693,那么我们称s为“厚积薄发数”;请求出所有“厚积薄发数”中M(s)的最大值.
相关试题

