【题目】已知关于x的一元二次方程![]()
![]() 求证:无论m取何值,方程总有两个不相等的实数根;
求证:无论m取何值,方程总有两个不相等的实数根;
![]() 若a和b是这个一元二次方程的两个根,求
若a和b是这个一元二次方程的两个根,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)证明见解析;(2)3.
【解析】
(1)根据方程的系数结合根的判别式,可得出△=m2+4>0,从而证出无论m取何值,原方程总有两个不相等的实数根;
(2)由根与系数的关系可得出a+b=﹣[﹣(m+2)],ab=m,结合a2+b2=(a+b)2﹣2ab解答.
(1)在关于x的一元二次方程x2﹣(m+2)x+m=0中a=1,b=﹣(m+2),c=m,
所以△=m2+4m+4﹣4m=m2+4,
无论m取何值,m2+4>0,
所以,无论m取何值,方程总有两个不相等的实数根;
(2)因为a和b是这个一元二次方程的两个根,
所以a+b=﹣[﹣(m+2)]=m+2,ab=m,
所以a2+b2=(a+b)2﹣2ab=(m+2)2﹣2m=m2+2m+4=(m+1)2+3.
无论m为何值,(m+1)2≥0,所以a2+b2的最小值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是由几个相同的小正方体搭成的几何体,
(1)搭成这个几何体需要 个小正方体;
(2)画出这个几何体的主视图和左视图;
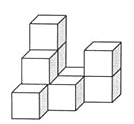
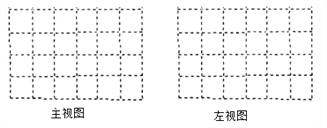
(3)在保持主视图和左视图不变的情况下,最多可以拿掉n个小正方体,则n= ,请在备用图中画出拿掉n个小正方体后新的几何体的俯视图.
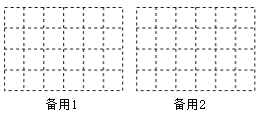
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,
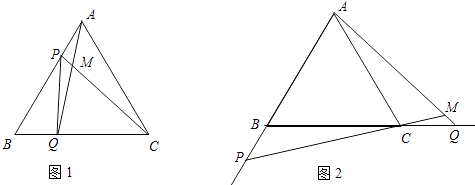
(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)何时△PBQ是直角三角形?
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个长为16,宽为8的矩形纸片先从下向上,再从左向右对折两次后,沿过所得矩形较长一边中点的直线剪掉一部分,再将剩下的打开,得到一个正方形,则这个正方形的面积是______.
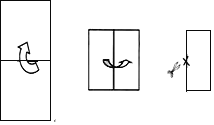
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.

(1)当m= 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,当CA⊥CP时,求m的值;
(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E恰好落在坐标轴上?若存在,请直接写出所有满足条件的点E的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
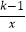 的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )
的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )
A.方程有两个不想等的实数根
B.方程不一定有实数根
C.方程有两个相等的实数根
D.方程没有实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
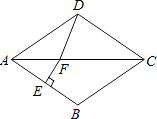
A.55°
B.65°
C.75°
D.85°
相关试题

