【题目】如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( ) 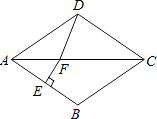
A.55°
B.65°
C.75°
D.85°
参考答案:
【答案】C
【解析】解:如图,连接BF, 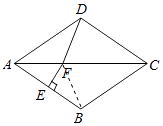
在菱形ABCD中,∠BAC= ![]() ∠BAD=
∠BAD= ![]() ×70°=35°,∠BCF=∠DCF,BC=DC,
×70°=35°,∠BCF=∠DCF,BC=DC,
∠ABC=180°﹣∠BAD=180°﹣70°=110°,
∵EF是线段AB的垂直平分线,
∴AF=BF,∠ABF=∠BAC=35°,
∴∠CBF=∠ABC﹣∠ABF=110°﹣35°=75°,
∵在△BCF和△DCF中,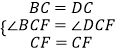 ,
,
∴△BCF≌△DCF(SAS),
∴∠CDF=∠CBF=75°,
故选C.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质和菱形的性质的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
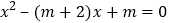
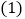 求证:无论m取何值,方程总有两个不相等的实数根;
求证:无论m取何值,方程总有两个不相等的实数根;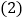 若a和b是这个一元二次方程的两个根,求
若a和b是这个一元二次方程的两个根,求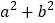 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.

(1)当m= 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,当CA⊥CP时,求m的值;
(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E恰好落在坐标轴上?若存在,请直接写出所有满足条件的点E的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
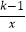 的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )
的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )
A.方程有两个不想等的实数根
B.方程不一定有实数根
C.方程有两个相等的实数根
D.方程没有实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的
 (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距200千米,一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,相向而行.已知客车的速度为60千米/小时,出租车的速度是100千米/小时.
(1)多长时间后两车相遇?
(2)若甲乙两地之间有相距50km的A、B两个加油站,当客车进入A站加油时,出租车恰好进入B站加油,求A加油站到甲地的距离.
(3)若出租车到达甲地休息10分钟后,按原速原路返回.出租车能否在到达乙地或到达乙地之前追上客车?若不能,则出租车往返的过程中,至少提速为多少才能在到达乙地或到达乙地之前追上客车?是否超速(高速限速为120千米/小时)?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为( )

A.
B.3
C.5
D.6
相关试题

