【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.
(1)当m= ![]() 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,当CA⊥CP时,求m的值;
(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E恰好落在坐标轴上?若存在,请直接写出所有满足条件的点E的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:当m= ![]() 时,y=﹣x2+5x;
时,y=﹣x2+5x;
令y=0,得﹣x2+5x=0.
∴x1=0,x2=5,
∴A(5,0).
当x=1时,y=4,
∴B(1,4).
∵抛物线y=﹣x2+5x的对称轴为直线x= ![]() ,
,
又∵点B,C关于对称轴对称,
∴BC=3
(2)
解:过点C作CH⊥x轴于点H(如图).

由已知得∠ACP=∠BCH=90°
∴∠ACH=∠PCB.
又∵∠AHC=∠PBC=90°,
tan∠ACH=tan∠PCB.
∴ ![]() .
.
∵抛物线y=﹣x2+2mx的对称轴为直线x=m,其中m>1,
又∵B,C关于对称轴对称,
∴BC=2(m﹣1).
∵B(1,2m﹣1),P(1,m),
∴BP=m﹣1.
又∵A(2m,0),C(2m﹣1,2m﹣1),
∴H(2m﹣1,0).
∴AH=1,CH=2m﹣1.
∴ ![]() ,
,
∴m= ![]() ;
;
(3)
解:存在.
∵B,C不重合,
∴m≠1,分两种情况:
①当m>1时,m=2,相对应的E点坐标是(2,0)或(0,4);
②当0<m<1时,m= ![]() .,相对应的E点坐标是(
.,相对应的E点坐标是( ![]() ,0);
,0);
∴E点坐标是(2,0)或(0,4)或( ![]() ,0)
,0)
【解析】(1)把m= ![]() ,代入抛物线的解析式,令y=0解方程,得到的非0解即为和x轴交点的横坐标,再求出抛物线的对称轴方程,进而求出BC的长;(2)过点C作CH⊥x轴于点H(如图1)由已知得∠ACP=∠BCH=90°,利用已知条件证明△ACH∽△PCB,根据相似的性质得到:
,代入抛物线的解析式,令y=0解方程,得到的非0解即为和x轴交点的横坐标,再求出抛物线的对称轴方程,进而求出BC的长;(2)过点C作CH⊥x轴于点H(如图1)由已知得∠ACP=∠BCH=90°,利用已知条件证明△ACH∽△PCB,根据相似的性质得到: ![]() ,再用含有m的代数式表示出BC,CH,BP,代入比例式即可求出m的值;(3)存在,本题要分当m>1时,BC=2(m﹣1),PM=m,BP=m﹣1和当0<m<1时,BC=2(1﹣m),PM=m,BP=1﹣m,两种情况分别讨论,再求出满足题意的m值和相对应的点E坐标.
,再用含有m的代数式表示出BC,CH,BP,代入比例式即可求出m的值;(3)存在,本题要分当m>1时,BC=2(m﹣1),PM=m,BP=m﹣1和当0<m<1时,BC=2(1﹣m),PM=m,BP=1﹣m,两种情况分别讨论,再求出满足题意的m值和相对应的点E坐标.
【考点精析】认真审题,首先需要了解相似三角形的应用(测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,
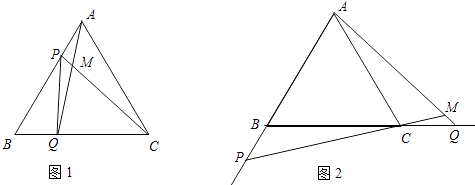
(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)何时△PBQ是直角三角形?
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数. -
科目: 来源: 题型:
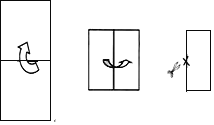
查看答案和解析>>【题目】如图,将一个长为16,宽为8的矩形纸片先从下向上,再从左向右对折两次后,沿过所得矩形较长一边中点的直线剪掉一部分,再将剩下的打开,得到一个正方形,则这个正方形的面积是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
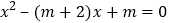
 求证:无论m取何值,方程总有两个不相等的实数根;
求证:无论m取何值,方程总有两个不相等的实数根;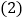 若a和b是这个一元二次方程的两个根,求
若a和b是这个一元二次方程的两个根,求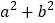 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
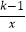 的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )
的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )
A.方程有两个不想等的实数根
B.方程不一定有实数根
C.方程有两个相等的实数根
D.方程没有实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
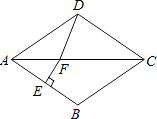
A.55°
B.65°
C.75°
D.85° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的
 (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

相关试题

