【题目】若方程组 ![]() 的解x,y满足0<x+y<1,则k的取值范围是( )
的解x,y满足0<x+y<1,则k的取值范围是( )
A.﹣4<k<0
B.﹣1<k<0
C.0<k<8
D.k>﹣4
参考答案:
【答案】A
【解析】解:∵0<x+y<1, 观察方程组可知,上下两个方程相加可得:4x+4y=k+4,
两边都除以4得,x+y= ![]() ,
,
所以 ![]() >0,
>0,
解得k>﹣4;![]() <1,
<1,
解得k<0.
所以﹣4<k<0.
故选A.
【考点精析】关于本题考查的解二元一次方程组和一元一次不等式组的解法,需要了解二元一次方程组:①代入消元法;②加减消元法;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是O的直径,点C在O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
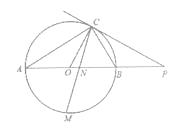
(1)求证:PC是O的切线;
(2)求证:BC= AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.

(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-6)-(-9); (2)1.8-(-2.6);
(3)
 ; (4)8-(9-10);
; (4)8-(9-10);(5)(-61)-(-71)-(-8)-(-2); (6)
 -3.7-(-
-3.7-(- )-1.3.
)-1.3. -
科目: 来源: 题型:
查看答案和解析>>【题目】小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,则下列说法不正确的是( )

A. 小刘家与超市相距3000米 B. 小刘去超市途中的速度是300米/分
C. 小刘在超市逗留了30分钟 D. 小刘从超市返回家比从家里去超市的速度快
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=
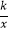 (k≠0)在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB﹣CE=1.直线l过O、E两点,则tan∠EOC的值为( )
(k≠0)在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB﹣CE=1.直线l过O、E两点,则tan∠EOC的值为( ) 
A.
B.5
C.
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法: ①abc<0;
②2a﹣b=0;
③4a+2b+c<0;
④若(﹣5,y1),( ,y2)是抛物线上两点,则y1>y2 .
,y2)是抛物线上两点,则y1>y2 .
其中说法正确的是( )
A.①②
B.②③
C.①②④
D.②③④
相关试题

