【题目】如图,已知AB是O的直径,点C在O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.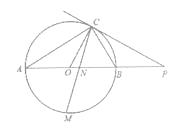
(1)求证:PC是O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
参考答案:
【答案】
(1)
证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)
证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= ![]() AB.
AB.
(3)
解:连接MA,MB,
∵点M是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴ ![]() ,
,
∴BM2=MNMC.
又∵AB是⊙O的直径, ![]() =
= ![]() ,
,
∴∠AMB=90°,AM=BM.
∵AB=4,
∴BM=2 ![]() .
.
∴MNMC=BM2=8.
【解析】(1)由半径OA=OC,可得等边对等角∠A=∠ACO,则∠COB=2∠A,已知∠COB=2∠PCB,∠A=∠ACO=∠PCB.由直径所对的圆周角是直角可得∠ACO+∠OCB=90°.从而转换得到∠PCB+∠OCB=90°即可证得;(2)“等角对等边”与“等边对等角”相互运用可证OC=BC;(3)连接MA,MB,先证明△MBN∽△MCB.则 ![]() ,即BM2=MNMC.由AB是⊙O的直径,
,即BM2=MNMC.由AB是⊙O的直径, ![]() =
= ![]() ,AB=4,解出BM,从而可解得MNMC.
,AB=4,解出BM,从而可解得MNMC.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上,
 =
=  ,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=
,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=  的图象过点C,若以CD为边的正方形的面积等于
的图象过点C,若以CD为边的正方形的面积等于  ,则k的值是.
,则k的值是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各项目的工作量如图所示:
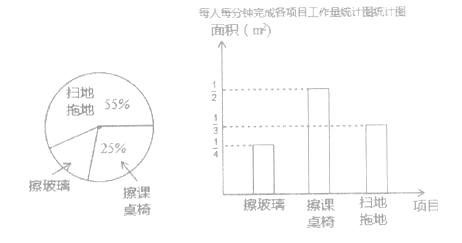
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为 , 每人每分钟擦课桌椅
m2;
(2)扫地拖地的面积是m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?(要有详细的解答过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】在ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.

(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.

(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-6)-(-9); (2)1.8-(-2.6);
(3)
 ; (4)8-(9-10);
; (4)8-(9-10);(5)(-61)-(-71)-(-8)-(-2); (6)
 -3.7-(-
-3.7-(- )-1.3.
)-1.3. -
科目: 来源: 题型:
查看答案和解析>>【题目】若方程组
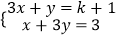 的解x,y满足0<x+y<1,则k的取值范围是( )
的解x,y满足0<x+y<1,则k的取值范围是( )
A.﹣4<k<0
B.﹣1<k<0
C.0<k<8
D.k>﹣4
相关试题

