【题目】我们约定:体重在选定标准的![]() %(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
%(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
体重 | 45 | 62 | 55 | 58 | 67 | 80 | 53 | 65 | 60 | 55 |
根据以上表格信息解决如下问题:
(1)将这组数据的三个统计量:平均数、中位数和众数填入下表:
平均数 | 中位数 | 众数 |
(2)请你选择其中一个统计量作为选定标准,说明选择的理由.并按此选定标准找出这10名男生中具有“一般体重”的男生.
参考答案:
【答案】(1)60,59,55;(1)见解析;
【解析】
(1)根据平均数、中位数和众数的定义分别进行计算,即可求出答案;
(2)根据选平均数作为标准,得出体重x满足![]() 为“普通体重”,从而得出②,④,⑨的男生的体重具有“普通体重”;
为“普通体重”,从而得出②,④,⑨的男生的体重具有“普通体重”;
根据选中位数作为标准,得出体重x满足![]() 为“普通体重”,从而得出④和⑨的男生的体重具有“普通体重”;
为“普通体重”,从而得出④和⑨的男生的体重具有“普通体重”;
根据选众数作为标准,得出体重x满足![]() 为“普通体重”,此时得出③、⑦、⑩的男生的体重具有“普通体重”.
为“普通体重”,此时得出③、⑦、⑩的男生的体重具有“普通体重”.
(1)这组数据按从小到大的顺序排列为:45,53,55,55,58,60,62,65,67,80,
则平均数为:![]() =60(kg);
=60(kg);
中位数为:![]() (kg);
(kg);
众数为:55;
故填表为:
平均数 | 中位数 | 众数 |
60 | 59 | 55 |
(2) i)选平均数作为标准.
理由:平均数刻画了一组数据的集中趋势,能够反映一组数据的平均水平.
当体重![]() 满足:
满足:![]()
即![]() 时为“一般体重”,
时为“一般体重”,
此时序号为②,④,⑨的男生具有“一般体重”.
ii)选中位数作为标准.
理由:中位数刻画了一组数据的集中趋势,且不受极端数据(如最小值45
和最大值80)的影响.
当体重![]() 满足:
满足:![]()
即![]() 时为“一般体重”,
时为“一般体重”,
此时序号为④和⑨的男生具有“一般体重”.
iii)选众数作为标准.
理由:众数刻画了一组数据的集中趋势,可以反映较多的人的实际情况.
当体重![]() 满足:
满足:
即![]() 时为“一般体重”,
时为“一般体重”,
此时序号为③,⑦,⑩的男生具有“一般体重”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是边长为4的正方形,点P是平面内一点.且满足BP⊥PC,现将点P绕点D顺时针旋转90度,则CQ的最大值=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个顶点的坐标分别为A(﹣5,0)、B(﹣2,3)、C(﹣1,0)
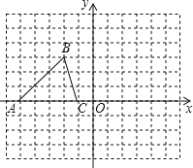
(1)画出△ABC向下平移3个单位的△A1B1C1;
(2)将△A1B1C1绕原点O旋转180°,画出旋转后的△A2B2C2;
(3)在(2)中,线段A1B1 扫过的面积为 .(设图中小正方的边长为1个单位长度)
-
科目: 来源: 题型:
查看答案和解析>>【题目】中考英语听力测试期间,需要杜绝考点周围的噪音
 如图,点A是我市一中考点,在位于A考点南偏西
如图,点A是我市一中考点,在位于A考点南偏西 方向距离120米的C点处有一消防队
方向距离120米的C点处有一消防队 在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东
在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东 方向的F点处突发火灾,消防队必须立即赶往救火
方向的F点处突发火灾,消防队必须立即赶往救火 已知消防车的警报声传播半径为110米,问消防车的警报声对听力测试是否会造成影响?若会造成影响,已知消防车行驶的速度为每小时60千米,则对听力测试的影响时间为几秒?
已知消防车的警报声传播半径为110米,问消防车的警报声对听力测试是否会造成影响?若会造成影响,已知消防车行驶的速度为每小时60千米,则对听力测试的影响时间为几秒? ,结果精确到1秒
,结果精确到1秒
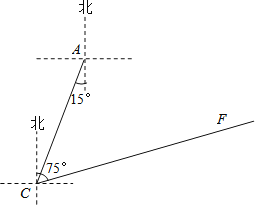
-
科目: 来源: 题型:
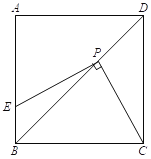
查看答案和解析>>【题目】如图,正方形ABCD的边长为6,点E是边AB上一点,点P是对角线BD上一点,且PE⊥PC.
⑴ 求证:PC=PE;
⑵ 若BE=2,求PB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司研发1000件新产品,需要精加工后才能投放市场.现在甲、乙两个工厂加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.25倍,公司需付甲工厂加工费用每天100元,乙工厂加工费用每天125元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)两个工厂同时合作完成这批产品,共付加工费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B﹣A﹣D﹣A运动,沿B﹣A运动时的速度为每秒13个单位长度,沿A﹣D﹣A运动时的速度为每秒8个单位长度.点Q从点 B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.
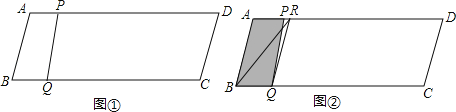
(1)当点P沿A﹣D﹣A运动时,求AP的长(用含t的代数式表示).
(2)连结AQ,在点P沿B﹣A﹣D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.
(3)过点Q作QR∥AB,交AD于点R,连结BR,如图②.在点P沿B﹣A﹣D运动过程中,当线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.
(4)设点C、D关于直线PQ的对称点分别为C′、D′,直接写出C′D′∥BC时t的值.
相关试题

