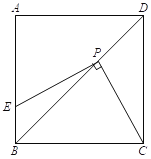
【题目】如图,正方形ABCD的边长为6,点E是边AB上一点,点P是对角线BD上一点,且PE⊥PC.
⑴ 求证:PC=PE;
⑵ 若BE=2,求PB的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
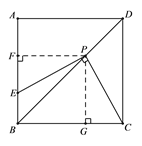
【解析】分析: ![]() 过点P作PF⊥AB,PG⊥BC,垂足分别为点F、G.证明△PFE≌△PGC即可.
过点P作PF⊥AB,PG⊥BC,垂足分别为点F、G.证明△PFE≌△PGC即可.
![]() 设EF=x.根据 △PFE≌△PGC .得到GC=EF=x. 由BE=2得:BF=x+2.
设EF=x.根据 △PFE≌△PGC .得到GC=EF=x. 由BE=2得:BF=x+2.
由正方形FBGP得:BG=x+2. BG+GC=6.列出方程,求出![]() ,在△PFB中,用勾股定理即可求出PB的长.
,在△PFB中,用勾股定理即可求出PB的长.
详解:⑴ 过点P作PF⊥AB,PG⊥BC,垂足分别为点F、G.
∴ ∠PFB=∠PGB=∠PGC=90°,
∵ 四边形ABCD是正方形,
∴ ∠A=∠ABC=90°,AB=AD=BC,
∴ ∠ABD=∠ADB=45°,四边形FBGP是矩形,
∴ ∠FPB=90°-∠ABD=90°-45°=45°,
∴ ∠ABD=∠FPB,
∴ FP=FB,
∴ 矩形FBGP是正方形,
∴ PF=PG,∠FPG=90°,
∴ ∠FPG+∠EPG=90°,
∵ EP⊥PC,
∴ ∠EPC=90°,
∴ ∠GPC+∠EPG=90°,
∴ ∠FPG=∠GPC ,
∵ ∠FPG=∠GPC ,PF=PG,∠PFE=∠PGC,
∴△PFE≌△PGC(ASA)
∴ PE=PC.
 (方法不唯一,酌情给分)
(方法不唯一,酌情给分)
⑵ 设EF=x.
∵ △PFE≌△PGC .
∴ GC=EF=x.
由BE=2得:BF=x+2.
由正方形FBGP得:BG=x+2.
∵ BC=6,
∴ BG+GC=6.
∴ (x+2)+x=6,
解得:x=2.
∴ PF=BF=2+2=4 ,
△PFB中,∠PFB=90°,由勾股定理得: ![]() ,
,
∵ PB>0
∴![]()
答:PB的长为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机张师傅某天上午营运全是在东西向的长江路上进行的,如果向东为正,向西为负,这天上午他行车里程(单位:km)如下:
 .
.⑴.最后一名乘客送到目的地,出租车在东面还是西面?在多少千米处?
⑵.请你帮张师傅算一下,这天上午他一共行驶了多少里程?
⑶.若每千米耗油0.1L,则这天上午张师傅一共用了多少升油?
-
科目: 来源: 题型:
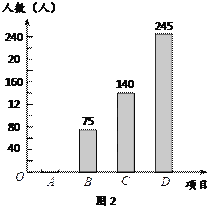
查看答案和解析>>【题目】某校在大课间中开设了A(体操),B(跑操),C(舞蹈),D(健美操)四项活动,为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:
⑴ 这次被调查的学生共有 人.
⑵ 请将统计图2补充完整.
⑶ 已知该校共有学生3400人,请根据调查结果估计该校喜欢健美操的学生人数.
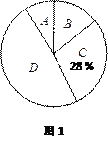
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华和小容都想参加学校组织的数学兴趣小组,根据学校分配的名额,他们两人只能有1人参加.数学老师想出了一个主意:如图,给他们六张卡片,每张卡片上都有一些数,将化简后的数在数轴上表示出来,再用“<”连接起来,谁先按照要求做对,谁就参加兴趣小组,你也一起来试一试吧!
-(-2) (-1)3 -|-3| 0的相反数
① ② ③ ④
-0.4的倒数 比-1大2.5的数
⑤ ⑥
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上,求这个长方形零件PQMN面积S的最大值.
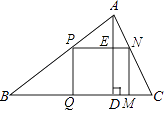
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值,
(1)2x2y﹣[3xy2+2(xy2+2x2y)],其中x=
 ,y=﹣2.
,y=﹣2.(2)已知a+b=4,ab=﹣2,求代数式(4a﹣3b﹣2ab)﹣(a﹣6b﹣ab)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
相关试题

