【题目】如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2 , 使A2B1=B1B2 , 以A2B2为边作等边△A2B2C2 , A3为等边
△A2B2C2的中心,连接A3B2并延长到点B3 , 使A3B2=B2B3 , 以A3B3为边作等边△A3B3C3 , 依次作下去得到等边△AnBnCn , 则等边△A5B5C5的边长为 . 
参考答案:
【答案】![]()
【解析】解:作A2D1⊥A1B1于D1 , A3D2⊥A2B2于D2 , 如图,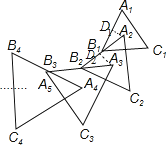
∵△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,
∴∠A2B1D1=30°,B1D1= ![]() A1B1=
A1B1= ![]() ,∴cos∠A2B1D1=cos30°=
,∴cos∠A2B1D1=cos30°= ![]() =
= ![]() ,∴A2B1=
,∴A2B1= ![]() ,
,
∵A2B1=B1B2 ,
∴A2B2= ![]() ,同理可得∠A3B2D2=30°,B2D2=
,同理可得∠A3B2D2=30°,B2D2= ![]() A2B2=
A2B2= ![]() ×
× ![]() =
= ![]() ,∴cos∠A3B2D2=cos30°=
,∴cos∠A3B2D2=cos30°= ![]() =
= ![]() ,∴A3B2=
,∴A3B2= ![]() ,
,
∵A3B2=B2B3 ,
∴A3B3= ![]() =(
=( ![]() )2=(
)2=( ![]() )2 , 同理可得A4B4=(
)2 , 同理可得A4B4=( ![]() )3 , A5B5=(
)3 , A5B5=( ![]() )4 . =
)4 . = ![]() 故答案为
故答案为 ![]() .
.
作A2D1⊥A1B1于D1 , A3D2⊥A2B2于D2 , 根据等边三角形的中心的性质得∠A2B1D1=30°,B1D1= ![]() A1B1=
A1B1= ![]() ,利用余弦的定义得cos∠A2B1D1=cos30°=
,利用余弦的定义得cos∠A2B1D1=cos30°= ![]() =
= ![]() ,可计算出A2B1=
,可计算出A2B1= ![]() ,由A2B1=B1B2得到A2B2=
,由A2B1=B1B2得到A2B2= ![]() ,用同样的方法可计算出A3B3=(
,用同样的方法可计算出A3B3=( ![]() )2 , 于是A4B4=(
)2 , 于是A4B4=( ![]() )3 , A5B5=(
)3 , A5B5=( ![]() )4 .
)4 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】(徐州中考)如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长交DC于点F,求证:
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=
 ,求AB的长。
,求AB的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正
 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰梯形OABC在平面直角坐标系中,如图A(1,2),B(3,2),C(4,0),则过点M(0,5)且把等腰梯形OABC面积分成相等两部分的直线解析式是

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度,在第二象限内有横、纵坐标均为整数的A、B两点,点B(﹣2,3),点A的横坐标为﹣2,且OA=
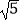 .
. 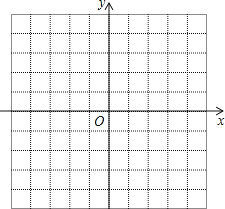
(1)直接写出A点的坐标,并连接AB,AO,BO;
(2)画出△OAB关于点O成中心对称的图形△OA1B1 , 并写出点A1、B1的坐标;(点A1、B1的对应点分别为A、B)
(3)将△OAB水平向右平移4个单位长度,画出平移后的△O1A2B2 .
相关试题

