搜索
【题目】如图，在四边形ABCD中，
，
，
，
，点E在AB边上，
，
．
求CE的长度；
求证：
≌
；
设点P是线段AB上的一个动点，求
的最小值是多少？
参考答案：
【答案】（1）5，（2）见解析，（3） 
的最小值为
．
【解析】
由
，
，
，根据勾股定理求出CE；
先证出
，即可证明
≌
；
作点D关于AB的对称点F，连接CF交AB于点P，再用勾股定理求出CF的长即为的最小值．
解：
，，，
根据勾股定理可得：
；
，
，
，
，
，
，，
，
在和中，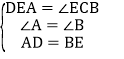
≌
；
延长DA至F，使得
，并连接CF，此时CF与AB的交点为点P，连接PD；
，且，
是等腰三角形，
，
的最小值为CF，
过点F作FH垂直CB的长线，垂足为H，如图所示：
根据题意得：
，
，
根据勾股定理可得，
，
即的最小值为．
故答案为：（1）5，（2）见解析，（3） 的最小值为．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：(1)∣—6∣+(
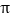—3.14)0—(
)-2+(—2)3 (2)(-a)3a2+(2a4)2÷a3.(3)
(4)(a-2b)(a+b)－3a(a+b) -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）先化简，再求值：(x-3)2+2(x-2)(x+7)-(x+2)(x-2)；其中x2+2x-3=0
（2）已知
，求: 
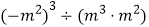的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】 “低碳生活，绿色出行”是我们倡导的一种生活方式，有关部门抽样调查了某单位员工上下班的交通方式，绘制了如下统计图：
（1）填空：样本中的总人数为 ；开私家车的人数m= ；扇形统计图中“骑自行车”所在扇形的圆心角为 度；
（2）补全条形统计图；
（3）该单位共有2000人，积极践行这种生活方式，越来越多的人上下班由开私家车改为骑自行车．若步行，坐公交车上下班的人数保持不变，问原来开私家车的人中至少有多少人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，长方形纸片ABCD，点E、F分别在边AB、CD上，连接EF，将∠BEF对折，点B落在直线EF上的B′处，得到折痕EC，将点A落在直线EF上的点A′处，得到折痕EN．
（1）若∠BEB′=110°，则∠BEC=°，∠AEN=°，∠BEC+∠AEN°．
（2）若∠BEB′=m°，则（1）中∠BEC+∠AEN的值是否改变？请说明你的理由．
（3）将∠ECF对折，点E刚好落在F处，且折痕与B′C重合，求∠DNA′． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，若∠A=15°，AB=BC=CD=DE=EF，则∠DEF等于__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣x2+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．
（1）直接写出A、B、C三点的坐标和抛物线的对称轴；
（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；
①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？
②设△BCF的面积为S，求S与m的函数关系式．
相关试题
