Question

【题目】如图，抛物线y=﹣x2+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．

（1）直接写出A、B、C三点的坐标和抛物线的对称轴；
（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；
①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？
②设△BCF的面积为S，求S与m的函数关系式．

Answer 1

【答案】
（1）解：A（﹣1，0），B（3，0），C（0，3）．

抛物线的对称轴是：直线x=1．

（2）解：①设直线BC的函数关系式为：y=kx+b．

把B（3，0），C（0，3）分别代入得：

解得： ．

所以直线BC的函数关系式为：y=﹣x+3．

当x=1时，y=﹣1+3=2，

∴E（1，2）．

当x=m时，y=﹣m+3，

∴P（m，﹣m+3）．

在y=﹣x2+2x+3中，当x=1时，y=4．

∴D（1，4）

当x=m时，y=﹣m2+2m+3，

∴F（m，﹣m2+2m+3）

∴线段DE=4﹣2=2，

线段PF=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m

∵PF∥DE，

∴当PF=ED时，四边形PEDF为平行四边形．

由﹣m2+3m=2，

解得：m1=2，m2=1（不合题意，舍去）．

因此，当m=2时，四边形PEDF为平行四边形．

②设直线PF与x轴交于点M，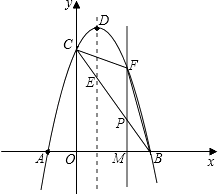

由B（3，0），O（0，0），

可得：OB=OM+MB=3．

∵S=S△BPF+S△CPF

即S= PFBM+ PFOM= PF（BM+OM）= PFOB．

∴S= ×3（﹣m2+3m）=﹣ m2+ m（0≤m≤3）．

∵B（3，0），C（0，3），D（1，4），

∴ ，

∴ ，

∵∠DEC=∠COB=90°，

∴△DEC∽△COB，

∴∠DCE=∠CBO，

∴∠DCE+∠OCB=90°，

∴DC⊥BC，

∴△BCD的外接圆圆心M为BD中点，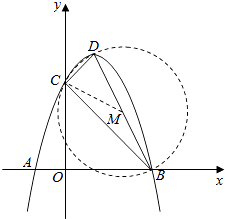

∴MX= =2，MY= =2，

∴△BCD的外接圆圆心M（2，2）

【解析】（1）与x轴交点令y=0,解方程即可，与y轴交点，令x=0，求出y即可，对称轴可套公式x=；（2）若四边形PEDF为平行四边形，可得PF∥DE,PF=ED,用m的代数式表示PF，等于DE的长，构建方程即可；（3）用分割的方法把三角形面积分成S△BPF+S△CPF，分别用m的代数式表示底边和高即可.