Question

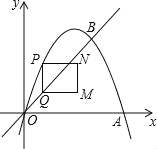
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx与x轴交于O、A两点，与直线y=x交于点B，点A、B的坐标分别为（3，0）、（2，2）．点P在抛物线上，过点P作y轴的平行线交射线OB于点Q，以PQ为边向右作矩形PQMN，且PN=1，设点P的横坐标为m（m＞0，且m≠2）．

（1）求这条抛物线所对应的函数表达式．

（2）求矩形PQMN的周长C与m之间的函数关系式．

（3）当矩形PQMN是正方形时，求m的值．

Answer 1

【答案】（1）y=﹣x2+3x．（2）①当0＜m＜2时，C=﹣2m2+4m+2．②当m＞2时，C=2m2﹣4m+2．（3）1或1+.

【解析】

试题分析: （1）把A（3，0）、B（2，2）两点坐标代入y=ax2+bx，解方程组即可解决．

（2）分两种情形：①0＜m＜2，②m＞2，分别求出矩形PQMN的周长C与m之间的函数关系式即可．

（3）分两种情形列出方程即可解决．

试题解析：（1）把A（3，0）、B（2，2）两点坐标代入y=ax2+bx，

得，解得．

故抛物线所对应的函数表达式为y=﹣x2+3x．

（2）∵点P在抛物线y=﹣x2+3x上，

∴可以设P（m，﹣m2+3m），

∵PQ∥y轴，

∴Q（m，m）．

①当0＜m＜2时，如图1中，

PQ=﹣m2+3m﹣m=﹣m2﹣2m，

C=2（﹣m2+2m）+2=﹣2m2+4m+2．

②当m＞2时，如图2中，

PQ=m﹣（﹣m2+3m）=m2﹣2m，

C=2（m2﹣2m）+2=2m2﹣4m+2．

（3）∵矩形PQMN是正方形，

∴PQ=PN=1，

当0＜m＜2时，如图3中，

﹣m2+2m=1，解得m=1．

当m＞2时，如图4中，

m2﹣2m=1，解得m=1+（或1﹣不合题意舍弃）．