【题目】下列各小题中,都有OE平分∠AOC,OF平分∠BOC.
(1)如图①,若点A、O、B在一条直线上,∠EOF= ;
(2)如图②,若点A、O、B不在一条直线上,∠AOB=140°,则∠EOF= ;
(3)由以上两个问题发现:当∠AOC在∠BOC的外部时,∠EOF与∠AOB的数量关系是∠EOF= ;
(4)如图③,若OA在∠BOC的内部,∠AOB和∠EOF还存在上述的数量关系吗?请简单说明理由;



参考答案:
【答案】(1)90°;(2)70°;(3)![]() ∠AOB;(4)存在.
∠AOB;(4)存在.
【解析】试题分析:(1)根据OE平分∠AOC,OF平分∠BOC,点A、O、B在一条直线上,即可得到∠EOF的度数;
(2)根据OE平分∠AOC,OF平分∠BOC,∠AOB=140°,即可得到∠EOF的度数;
(3)根据(2)中的方法,即可得到∠EOF与∠AOB的数量关系;
(4)若OA在∠BOC的内部,∠AOB和∠EOF还存在上述的数量关系,方法同(3).
试题解析:解:(1)∵OE平分∠AOC,OF平分∠BOC,∴∠COF=![]() ∠COB;∠COE=
∠COB;∠COE=![]() ∠AOC,又∵∠AOB=180°,∴∠EOF=
∠AOC,又∵∠AOB=180°,∴∠EOF=![]() ∠COB+
∠COB+![]() ∠AOC=
∠AOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=90°;
∠AOB=90°;
(2)∵OE平分∠AOC,OF平分∠BOC,∴∠COF=![]() ∠COB;∠COE=
∠COB;∠COE=![]() ∠AOC,又∵∠AOB=140°,∴∠EOF=
∠AOC,又∵∠AOB=140°,∴∠EOF=![]() ∠COB+
∠COB+![]() ∠AOC=
∠AOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=70°;
∠AOB=70°;
(3)∵OE平分∠AOC,OF平分∠BOC,∴∠COF=![]() ∠COB;∠COE=
∠COB;∠COE=![]() ∠AOC,∴∠EOF=
∠AOC,∴∠EOF=![]() ∠COB+
∠COB+![]() ∠AOC=
∠AOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB;
∠AOB;
(4)存在.
∵OF平分∠BOC,OE平分∠AOC,∴∠COF=![]() ∠COB;∠COE=
∠COB;∠COE=![]() ∠AOC;
∠AOC;
∴∠EOF=![]() ∠COB﹣
∠COB﹣![]() ∠AOC=
∠AOC=![]() (∠BOC﹣∠AOC)=
(∠BOC﹣∠AOC)=![]() ∠AOB.
∠AOB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B、C在同一条直线上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点.
(1)画出符合题意的图形;
(2)依据(1)的图形,求线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是 ;
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;

(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且
 =
= 时,直接写出线段CE的长.
时,直接写出线段CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
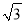 的坡面AB向上行走到B处,测得广告牌顶部C的仰角为45°,又知AB=10m,AE=15m,求广告牌CD的高度(精确到0.1m,测角仪的高度忽略不计)
的坡面AB向上行走到B处,测得广告牌顶部C的仰角为45°,又知AB=10m,AE=15m,求广告牌CD的高度(精确到0.1m,测角仪的高度忽略不计)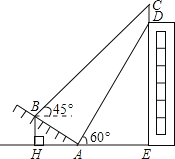
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点F是等边△ABC的边BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与等边△ABC在BC的同侧,且CD∥AB,连结BE.

(1)如图①,若AB=10,EF=8,请计算△BEF的面积;
(2)如图②,若点G是BE的中点,连接AG、DG、AD.试探究AG与DG的位置和数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边长分别为10和2,第三边的数值是偶数,则第三边长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接任意四边形的各边中点得到的四边形一定是( )
A.正方形
B.矩形
C.菱形
D.平行四边形
相关试题

