【题目】顺次连接任意四边形的各边中点得到的四边形一定是( )
A.正方形
B.矩形
C.菱形
D.平行四边形
参考答案:
【答案】D
【解析】解:连接BD, 已知任意四边形ABCD,E、F、G、H分别是各边中点.
在△ABD中,E、H是AB、AD中点,
所以EH∥BD,EH= ![]() BD.
BD.
在△BCD中,G、F是DC、BC中点,
所以GF∥BD,GF= ![]() BD,
BD,
所以EH=GF,EH∥DF,
所以四边形EFGH为平行四边形.
故选D.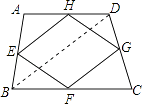
【考点精析】根据题目的已知条件,利用三角形中位线定理和平行四边形的判定的相关知识可以得到问题的答案,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)2017+(3.14﹣π)0+2﹣1 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
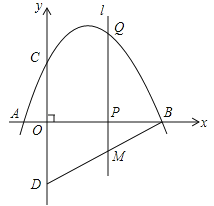
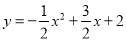 与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.(1)求点A、点B、点C的坐标;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(4)在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】底面半径为10cm,高为40cm的圆柱形水桶中装满了水。小明先将桶中的水倒满3个底面半径为3cm,高为5cm的圆柱形杯子,如果剩下的水倒在长、宽、高分别为50cm,20cm和12cm的长方体容器内,会满出来吗?若没有满出来,求出长方体容器内水的高度(
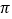 取3)。
取3)。 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题为假命题的是( )
A. 三角形三个内角的和等于180° B. 三角形两边之和大于第三边
C. 三角形的外角大于任何一个和它不相邻的内角 D. 若a>0,b<0,则a+b>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( )

A.15°
B.20°
C.25°
D.30° -
科目: 来源: 题型:
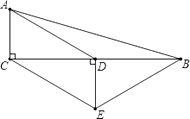
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,则四边形ACEB的周长为 .
相关试题

