【题目】如图,△ABC 和△CDE 都是等腰直角三角形,∠ACB=∠ECD=90°,D 为 AB 边上一点.如下结论:

①△ACE≌△BCD; ②△ADE 是直角三角形; ③AD2+BD2=2CD2; ④AE=AC, 其中正确的结论有( )
A.①③④B.①②③C.①②D.①③
参考答案:
【答案】B
【解析】
由△ABC 和△CDE是等腰直角三角形,则BC=AC,CE=CD,由∠ACB=∠ECD=90°,得到∠ACE=∠BCD,则△ACE≌△BCD;则∠CAE=∠B=45°,则得到∠EAD=90°;由AE=BD,则AD2+BD2= AD2+AE2=ED2,由ED2=CD2+CE2=2CD2;无法证明AE=AC,即可得到答案.
解:∵△ABC 和△CDE是等腰直角三角形,
∴BC=AC,CE=CD,∠B=∠CAB=45°,
∵∠ACB=∠ECD=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD=90°,
∴∠ACE=∠BCD,
∴△ACE≌△BCD;故①正确;
∴∠CAE=∠B=45°,
∴∠CAE+∠CAB=90°,
∴∠EAD=90°,
∴△ADE是直角三角形;故②正确;
在直角三角形ADE中,AD2+AE2=ED2,
∵△ACE≌△BCD,
∴AE=BD,
∴AD2+BD2= ED2,
∵ED2=CD2+CE2=2CD2,
∴AD2+BD2=2CD2;故③正确;
无法正确AE=AC;故④错误;
∴正确的有:①②③;
故选择:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
(1)求证:∠BCP=∠BAN.
(2)若AC=4,PC=3,求MNBC的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践:
如图1,已知△ABC为等边三角形,点D,E分别在边AB、AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:在图1中,线段PM与PN的数量关系是 ,∠MPN的度数是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,
①判断△PMN的形状,并说明理由;
②求∠MPN的度数;
(3)拓展延伸:若△ABC为直角三角形,∠BAC=90°,AB=AC=10,点DE分别在边AB,AC上,AD=AE=4,连接DC,点M,P,N分别为DE,DC,BC的中点.把△ADE绕点A在平面内自由旋转,如图3,请直接写出△PMN面积的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:关于x的二次函数
 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=
 AC,连接CE、OE,连接AE,交OD于点F,若AB=2,∠ABC=600,则AE的长为( )
AC,连接CE、OE,连接AE,交OD于点F,若AB=2,∠ABC=600,则AE的长为( )
A.
 B.
B. 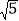 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(m-2)x+m+1=0有两个相等的实数根,则m的
值是
A. 0 B. 8 C. 4±2
 D. 0或8
D. 0或8 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件。若商场平均每天要盈利1600元,每件衬衫应降价多少元?
相关试题

