Question

【题目】综合与实践：

如图1，已知△ABC为等边三角形，点D，E分别在边AB、AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点．

（1）观察猜想：在图1中，线段PM与PN的数量关系是　 　，∠MPN的度数是　 　；

（2）探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，

①判断△PMN的形状，并说明理由；

②求∠MPN的度数；

（3）拓展延伸：若△ABC为直角三角形，∠BAC=90°，AB=AC=10，点DE分别在边AB，AC上，AD=AE=4，连接DC，点M，P，N分别为DE，DC，BC的中点．把△ADE绕点A在平面内自由旋转，如图3，请直接写出△PMN面积的最大值．

Answer 1

【答案】（1）PM=PN；120°；（2）①△PMN是等腰三角形，理由见解析；②120°；（3） ；

【解析】

(1)根据三角形中位线的性质可证明PN∥BD，PM∥EC，PN=BD，PM=CE，由AD=AE即可证明PM=PN，根据平行线性质及外角性质可证明∠MPN=∠B+∠ACB=120°；（2）①连接BD、CE，可证明△BAD≌△CAE，可知BD=CE，∠ABD=∠ACE，根据三角形中位线可知PN∥BD，PM∥EC，PN=BD，PM=CE，可知PN=PM即可判断△PMN是等腰三角形．②由平行线的性质可知∠PNC=∠DBC，∠DPM=∠A=ECD，进而可求出∠MPN=120°，（3）由旋转知，∠BAD=∠CAE，可证明△ABD≌△ACE（SAS），可知∠ABD=∠ACE，BD=CE，通过（2）的方法可证PM=PN，∠DPM=∠DCE，∠PNC=∠DBC

根据外角性质可证明∠MPN=∠ABC+∠ACB，进而可知△PMN是等腰直角三角形，求△PMN面积的最大值即可.

（1）如图1中，

∵AB=AC=BC，AD=AE，

∴BD=CE，∠B=∠ACB=60°，

∵点M，P，N分别为DE，DC，BC的中点，

∴PN∥BD，PM∥EC，PN=BD，PM=CE，

∴PN=PM，∠PNC=∠B，∠DPM=∠ACD，

∴∠MPN=∠MPD+∠DPN=∠ACD+∠PNC+∠DCB=∠ACD+∠DCB+∠B=∠ACB+∠B=120°，

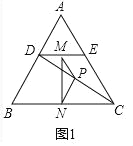
故答案为PM=PN，120°．

（2）如图2中，连接BD、EC．

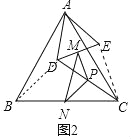
①∵∠BAC=∠DAE=60°，

∴∠BAD=∠CAE，

∵BA=CA，DA=EA，

∴△BAD≌△CAE，

∴BD=CE，∠ABD=∠ACE，

∵点M，P，N分别为DE，DC，BC的中点，

∴PN∥BD，PM∥EC，PN=BD，PM=CE，

∴PN=PM，

∴△PMN是等腰三角形．

②∵PN∥BD，PM∥EC

∴∠PNC=∠DBC，∠DPM=∠A=ECD，

∴∠MPN=∠MPD+∠DPN=∠ECD+∠PNC+∠DCB=∠ECD+∠DCB+∠DBC=∠ACE+ACD+∠DCB+∠DBC=∠ABD+∠ACB+∠DBC=∠ACB+∠ABC=120°．

（3）如图3中，

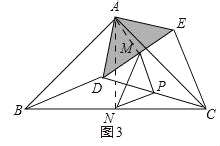
由旋转知，∠BAD=∠CAE，

∵AB=AC，AD=AE，

∴△ABD≌△ACE（SAS），

∴∠ABD=∠ACE，BD=CE，

同（2）的方法，利用三角形的中位线得，PN=BD，PM=CE，

∴PM=PN，

同（2）的方法得，PM∥CE，

∴∠DPM=∠DCE，

同（2）的方法得，PN∥BD，

∴∠PNC=∠DBC

∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，

∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC

=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC

=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC，

∵∠BAC=90°，

∴∠ACB+∠ABC=90°，

∴∠MPN=90°，

∴△PMN是等腰直角三角形，

∵PM=PN=BD，

∴BD最大时，PM最大，△PMN面积最大，

∴点D在BA的延长线上，

∴BD=AB+AD=14，

∴PM=7，

∴S△PMN最大=PM2=×72=.