【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行,且经过点(2,6).
(1)求一次函数y=kx+b的表达式.
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标,并在直角坐标系中画出这个函数的图象.

参考答案:
【答案】(1)一次函数表达式为:y=x+4;(2)与x轴交点坐标是(-4,0),与y轴交点分别是(0,4),画图象见解析.
【解析】
(1)由两直线平行即可得出k值,再由一次函数图象上点的坐标特征即可得出b的值,此题得解;
(2)将x=0、y=0分别代入一次函数解析中求出y、x值即可得出交点坐标,再在平面直角坐标系中画出图象即可.
(1)∵y=kx+b的图象与y=x-1的图象平行
∴k=1
即y=x+b
把(2,6)代入得:2+b=6, b=4
∴此一次函数表达式为:y=x+4
(2)y=x+4中,令y=0,则x+4=0,x= -4,得图象与x轴交点坐标是(-4,0)
令x=0,则y=4,得图象与y轴交点分别是(0,4)
在平面直角坐标系中画出图象如图所示,

-
科目: 来源: 题型:
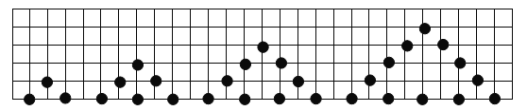
查看答案和解析>>【题目】如图,用棋盘摆出下列一组三角形,三角形每边有
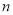 枚棋子,每个三角形的棋子总数是
枚棋子,每个三角形的棋子总数是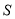 .
.
(1)求
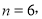 时
时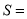 ;
;(2)按此规律推断,当三角形边上有
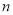 枚棋子时,该三角形的棋子总数
枚棋子时,该三角形的棋子总数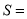 (用含
(用含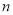 的代数式表示);
的代数式表示);(3)当三角形一边上有25枚棋子时,该三角形的棋子总数
 等于多少?
等于多少?(4)当三角形的棋子总数是123枚时,该三角形一边上的棋子数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电压力锅生产厂家计划每天平均生产n台电压力锅,而实际产量与计划产量相比有出入.下表记录了某周五个工作日每天实际产量情况(超过计划产量记为正、少于计划产量记为负):
星期
一
二
三
四
五
实际生产量/台
+5
-2
-4
+13
-3
(1)用含n的代数式表示本周前三天生产电压力锅的总台数;
(2)该厂实行每日计件工资制:每生产一台电压力锅可得60元,若超额完成任务,则超过部分每台1另奖10元;少生产一台扣15元.当n=100时,那么该厂工人这一周的工资总额是多少元?
(3)若将上面第(2)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,当n=100时,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
 ,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
-
科目: 来源: 题型:
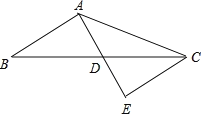
查看答案和解析>>【题目】如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,延长AD到点E,使DE=AD,连接CE.
(1)求证:△AEC是直角三角形.
(2)求BC边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求
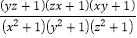 的值.
的值.
相关试题

