搜索
【题目】附加题：（y﹣z）2+（x﹣y）2+（z﹣x）2=（y+z﹣2x）2+（z+x﹣2y）2+（x+y﹣2z）2．
求
的值．
参考答案：
【答案】1.
【解析】分析：利用等式的性质将（y﹣z）2+（x﹣y）2+（z﹣x）2=（y+z﹣2x）2+（z+x﹣2y）2+（x+y﹣2z）2变形成（x﹣y）2+（x﹣z）2+（y﹣z）2=0的形式，从而得到x=y=z，再求得
的值.
详解：
∵（y﹣z）2+（x﹣y）2+（z﹣x）2=（y+z﹣2x）2+（z+x﹣2y）2+（x+y﹣2z）2．
∴（y﹣z）2﹣（y+z﹣2x）2+（x﹣y）2﹣（x+y﹣2z）2+（z﹣x）2﹣（z+x﹣2y）2=0，
∴（y﹣z+y+z﹣2x）（y﹣z﹣y﹣z+2x）+（x﹣y+x+y﹣2z）（x﹣y﹣x﹣y+2z）+（z﹣x+z+x﹣2y）（z﹣x﹣z﹣x+2y）=0，
∴2x2+2y2+2z2﹣2xy﹣2xz﹣2yz=0，
∴（x﹣y）2+（x﹣z）2+（y﹣z）2=0．
∵x，y，z均为实数，
∴x=y=z．
∴=
=1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行，且经过点(2，6)．
(1)求一次函数y=kx+b的表达式．
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标，并在直角坐标系中画出这个函数的图象．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（
，0），B（0，2），则B2的坐标为_____；点B2016的坐标为_____．
-
科目： 来源： 题型：
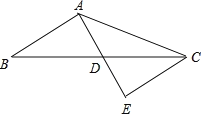
查看答案和解析>>【题目】如图，在△ABC中，AB=6，AC=10，AD是BC边上的中线，且AD=4，延长AD到点E，使DE=AD，连接CE．
(1)求证：△AEC是直角三角形．
(2)求BC边的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一蓄水池有水40m3,按一定的速度放水，水池里的水量y (m3)与放水时间t(分)有如下关系：
放水时间(分)
1
2
3
4
...
水池中水量(m)
38
36
34
32
...
下列结论中正确的是
A. y随t的增加而增大B. 放水时间为15分钟时，水池中水量为8m3
C. 每分钟的放水量是2m3D. y与t之间的关系式为y=38-2t
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是矩形，把矩形沿AC折叠，点B落在点E处，AE与DC的交点为O，连接DE．
（1）求证：△ADE≌△CED；
（2）求证：DE∥AC．
-
科目： 来源： 题型：
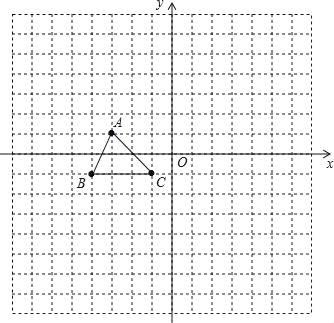
查看答案和解析>>【题目】如图，点A、B、C的坐标分别为（﹣3，1）、（﹣4，﹣1）、（﹣1，﹣1），将△ABC先向下平移2个单位，得△A1B1C1；再将△A1B1C1沿y轴翻折180°，得△A2B2C2；．
（1）画出△A1B1C1和△A2B2C2；
（2）求直线A2A的解析式．
相关试题
