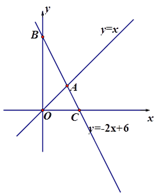
【题目】如图,直线![]() 与x轴、
与x轴、![]() 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线![]() 相交于
相交于
点A.
(1)点B、点C和点A的坐标分别是(0, )、( ,0)、( , );
(2)求两条直线与![]() 轴围成的三角形的面积;
轴围成的三角形的面积;
(3)在坐标轴上是否存在一点Q,使△OAQ的面积等于6,若存在请直接写出Q点的坐标,若不存在,请说明理由.
参考答案:
【答案】(1) 6,3,2,2;(2)3;(3)存在,理由见解析.
【解析】分析:(1)根据坐标轴上点的坐标特征易得B点坐标为(0,6),C点坐标为(3,0),然后解方程组![]() 可确定A点坐标;(2)根据三角形面积公式计算;(3)分类讨论:当Q点在x轴上,设Q(a,0),则S△AOQ=
可确定A点坐标;(2)根据三角形面积公式计算;(3)分类讨论:当Q点在x轴上,设Q(a,0),则S△AOQ=![]() ×2×|a|=6;当Q点在y轴上,设Q(0,b),则S△AOQ=
×2×|a|=6;当Q点在y轴上,设Q(0,b),则S△AOQ=![]() ×2×|b|=6,然后分别求出a和b的值,从而得到Q点的坐标.
×2×|b|=6,然后分别求出a和b的值,从而得到Q点的坐标.
本题解析:
(1)把x=0代入y=2x+6得y=6,所以B点坐标为(0,6),
把y=0代入y=2x+6得2x+6=0,解得x=3,所以C点坐标为(3,0),
解方程组![]() 得
得![]() ,所以A点坐标为(2,2),
,所以A点坐标为(2,2),
故答案为6,3,2,2;
(2) ![]() =
=![]() ×3×2=3;
×3×2=3;
(3)存在。
当Q点在x轴上,设Q(a,0),则S△AOQ=![]() ×2×|a|=6,
×2×|a|=6,
解得a=±6,
则Q点坐标为(6,0)、(6,0);
当Q点在y轴上,设Q(0,b),则![]() =
=![]() ×2×|b|=6,
×2×|b|=6,
解得b=±6,
则Q点坐标为(0,6)、(0,6),
综上所述Q点坐标为(0,6)、(0,6)、(6,0)、(6,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016浙江省舟山市第21题)如图,已知一次函数y1=kx+b的图象与反比例函数y2=
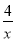 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=
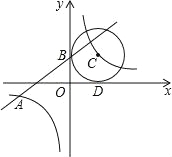
的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=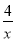 的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B(1)、求m的值;
(2)、求一次函数的表达式;
(3)、根据图象,当y1<y2<0时,写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别
频数(人数)
频率
小说
0.5
戏剧
4
散文
10
0.25
其他
6
合计
1
根据图表提供的信息,解答下列问题:
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣8x﹣1=0配方后可变形为( )
A.(x+4)2=17
B.(x﹣4)2=17
C.(x+4)2=15
D.(x﹣4)2=15 -
科目: 来源: 题型:
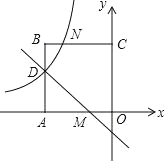
查看答案和解析>>【题目】(2016山东省泰安市第25题)如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=
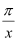 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N. (1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在∠AOB的两边上截取AO=BO,OC=OD,连接AD、BC交于点P,连接OP,则下列结论正确的是 ( )
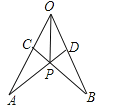
①△APC≌△BPD ②△ADO≌△BCO ③△AOP≌△BOP ④△OCP≌△ODP
A. ②③④ B. ①②③ C. ①②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个连续自然数的积为240,则这两个数是_____.
相关试题

