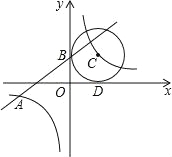
【题目】(2016浙江省舟山市第21题)如图,已知一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=
的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=![]() 的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
(1)、求m的值;
(2)、求一次函数的表达式;
(3)、根据图象,当y1<y2<0时,写出x的取值范围.
参考答案:
【答案】(1)、-1;(2)、y=![]() x+2;(3)、x<﹣4.
x+2;(3)、x<﹣4.
【解析】
试题分析:(1)、直接将A点代入反比例函数解析式求出答案;(2)、直接利用切线的性质结合正方形的判定与性质得出C,B点坐标,进而利用待定系数法求出一次函数解析式;(3)、利用A点坐标结合函数图象得出x的取值范围.
试题解析:(1)、把点A(﹣4,m)的坐标代入y2=![]() , 则m=4÷(-4)=﹣1, 得m=﹣1;
, 则m=4÷(-4)=﹣1, 得m=﹣1;
(2)、连接CB,CD, ∵⊙C与x轴,y轴相切于点D,B, ∴∠CBO=∠CDO=90°=∠BOD,BC=CD,
∴四边形BODC是正方形, ∴BO=OD=DC=CB, ∴设C(a,a)代入y2=![]() 得:a2=4,
得:a2=4,
∵a>0,∴a=2, ∴C(2,2),B(0,2),
把A(﹣4,﹣1)和(0,2)的坐标代入y1=kx+b中, 得:![]() , 解得:
, 解得:![]() ,
,
∴一次函数的表达式为:y1=![]() x+2;
x+2;
(3)/∵A(﹣4,﹣1),
∴当y1<y2<0时,x的取值范围是:x<﹣4.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱心一日捐”活动中,某校初三级部六个班的捐款数(单位:元)分别为520,460,480,560,580,600,则这组数据的极差是_________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y (元),生产A产品x (件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两千多年前,古希腊数学家欧几里得首次运用某种数学思想整理了几何知识,完成 了数学著作《原本》,欧几里得首次运用的这种数学思想是( )
A.公理化思想B.数形结合思想C.抽象思想D.模型思想
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别
频数(人数)
频率
小说
0.5
戏剧
4
散文
10
0.25
其他
6
合计
1
根据图表提供的信息,解答下列问题:
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣8x﹣1=0配方后可变形为( )
A.(x+4)2=17
B.(x﹣4)2=17
C.(x+4)2=15
D.(x﹣4)2=15 -
科目: 来源: 题型:
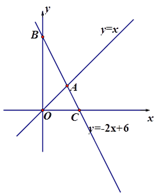
查看答案和解析>>【题目】如图,直线
 与x轴、
与x轴、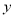 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线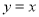 相交于
相交于点A.
(1)点B、点C和点A的坐标分别是(0, )、( ,0)、( , );
(2)求两条直线与
 轴围成的三角形的面积;
轴围成的三角形的面积;(3)在坐标轴上是否存在一点Q,使△OAQ的面积等于6,若存在请直接写出Q点的坐标,若不存在,请说明理由.
相关试题

